
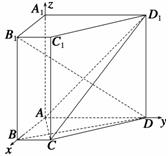
如图,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,A1C1⊥B1D ,BC=1,AD=AA1=3.
(Ⅰ)证明:平面ACD1⊥平面B1BDD1;
(Ⅱ)求直线B1C1与平面ACD1所成角的正弦值.
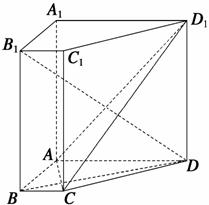
方法一 (1)证明
∵ AA1∥CC1且AA1=CC1,∴AC∥A1C1
∵A1C1⊥B1D ,∴AC⊥B1D
因为BB1⊥平面ABCD,AC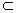 平面ABCD,所以AC⊥BB1. ,
平面ABCD,所以AC⊥BB1. ,
所以AC⊥平面B1BDD1 又因为AC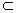 面ACD1, 平面ACD1⊥平面B1BDD1;
面ACD1, 平面ACD1⊥平面B1BDD1;
(2)解 因为B1C1∥AD,所以直线B1C1与平面ACD1所成的角等于直线AD与平面ACD1所成的角(记为θ).如图,连接A1D,因为棱柱ABCD-A1B1C1D1是直棱柱,且∠B1A1D1=∠BAD=90°,
所以A1B1⊥平面ADD1A1,从而A1B1⊥AD1.又AD=AA1=3,所以四边形ADD1A1是正方形.
于是A1D⊥AD1,故AD1⊥平面A1B1D,于是AD1⊥B1D.
由(1)知,AC⊥B1D,所以B1D⊥平面ACD1.故∠ADB1=90°-θ,在直角梯形ABCD中,
因为AC⊥BD,所以∠BAC=∠ADB.从而Rt△ABC∽Rt△DAB,故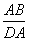 =
=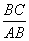 ,
,
即AB=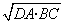 =
=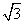 .
.
连接AB1,易知△AB1D是直角三角形,且B1D2=BB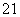 +BD2=BB
+BD2=BB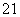 +AB2+AD2=21,
+AB2+AD2=21,
即B1D=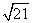 .在Rt△AB1D中,cos∠ADB1=
.在Rt△AB1D中,cos∠ADB1=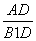 =
=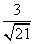 =
=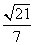 ,
,
即cos(90°-θ)=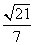 .
.
从而sin θ=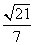 . 即直线B1C1与平面ACD1所成角的正弦值为
. 即直线B1C1与平面ACD1所成角的正弦值为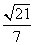 .
.
方法二 (1)证明 易知,AB,AD,AA1两两垂直.如图,以A为坐标原点,AB,AD,AA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系.
设AB=t,则相关各点的坐标为A(0,0,0),B(t,0,0),B1(t,0,3), C(t,1,0),C1(t,1,3),D(0,3,0),D1(0,3,3).
 从而
从而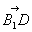 =(-t,3,-3),
=(-t,3,-3),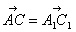 =(t,1,0),
=(t,1,0),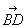 =(-t,3,0).
=(-t,3,0).
因为AC⊥BD,所以·-t2+3+0=0,解得t=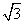 或t=-
或t=-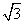 (舍去).
(舍去).
于是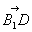 =(-
=(-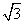 ,3,-3),
,3,-3),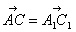 =(
=(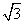 ,1,0),
,1,0),
因为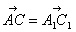
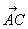
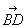 =-3+3+0=0, 所以⊥,即AC⊥B1D.
=-3+3+0=0, 所以⊥,即AC⊥B1D.
因为BB1⊥平面ABCD,AC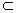 平面ABCD,
平面ABCD,
所以AC⊥BB1. ,所以AC⊥平面B1BDD1
又因为AC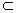 面ACD1, 平面ACD1⊥平面B1BDD1;
面ACD1, 平面ACD1⊥平面B1BDD1;
(2)解 由(1)知,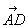 =(0,3,3),
=(0,3,3),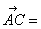 =(
=(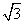 ,1,0),
,1,0),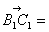 =(0,1,0).
=(0,1,0).
设n=(x,y,z)是平面ACD1的一个法向量,则,即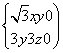
令x=1,则n=(1,-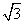 ,
,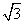 ).设直线B1C1与平面ACD1所成角为θ,则
).设直线B1C1与平面ACD1所成角为θ,则
sin θ=|cos〈n,〉|==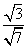 =
=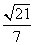 .
.
即直线B1C1与平面ACD1所成角的正弦值为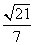 .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
已知曲线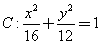 ,直线
,直线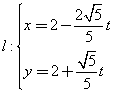 (
(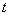 为参数)
为参数)
(I)写出曲线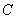 的参数方程,直线
的参数方程,直线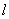 的普通方程;
的普通方程;
(II)过曲线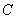 上任意一点
上任意一点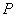 作与
作与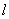 夹角为30°的直线,交
夹角为30°的直线,交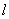 于点
于点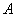 ,求
,求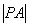 的最大值及此时P点的坐标。
的最大值及此时P点的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
在平面直角坐标系中,曲线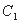 的参数方程为
的参数方程为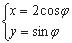 (
( 为参数),以
为参数),以 为极点,
为极点,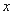 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 是圆心在极轴上且经过极点的圆,射线
是圆心在极轴上且经过极点的圆,射线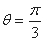 与曲线
与曲线 交于点
交于点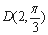
(1)求曲线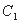 ,
, 的方程;
的方程;
(2)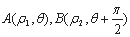 是曲线
是曲线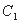 上的两点,求
上的两点,求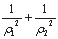 的值;
的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com