
分析 (1)通过将点P($\sqrt{3}$,$\frac{\sqrt{3}}{2}$)代入椭圆方程,利用$\frac{c}{a}$=$\frac{1}{2}$及b2+c2=a2,计算即得结论;
(2)分直线l斜率不存在、存在两种情况讨论.当直线的斜率存在时设其方程为y=k(x-1)并与同意方程联立,利用韦达定理、两点间距离公式及椭圆定义,计算$\frac{|AB|}{|AF|•|BF|}$即可.
解答 解:(1)由椭圆E过点P($\sqrt{3}$,$\frac{\sqrt{3}}{2}$),可得$\frac{3}{{a}^{2}}$+$\frac{3}{4{b}^{2}}$=1,
又e=$\frac{c}{a}$=$\frac{1}{2}$,b2+c2=a2,
解得:a=2,b=$\sqrt{3}$.
∴椭圆E方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)结论:存在实数$λ=\frac{4}{3}$,使得|AF|+|BF|=λ|AF|•|BF|恒成立.
理由如下:
若直线l斜率不存在,则可得A(1,$\frac{3}{2}$)、B(1,-$\frac{3}{2}$),
于是λ=$\frac{|AF|+|BF|}{|AF|•|BF|}$=$\frac{1}{|AF|}$+$\frac{1}{|BF|}$=$\frac{2}{3}$+$\frac{2}{3}$=$\frac{4}{3}$;
若直线的斜率存在,设其方程为:y=k(x-1),
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-1)}\end{array}\right.$,可得(3+4k2)x2-8k2x+(4k2-12)=0,
设A(x1,y1),B(x2,y2),由韦达定理可得:
x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
∵|AB|=$\sqrt{1+{k}^{2}}$|x2-x1|=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
|AF|•|BF|=$\sqrt{({x}_{1}-1)^{2}+{{y}_{1}}^{2}}$•$\sqrt{({x}_{2}-1)^{2}+{{y}_{2}}^{2}}$
=$\sqrt{({x}_{1}-1)^{2}+{k}^{2}({x}_{1}-1)^{2}}$•$\sqrt{({x}_{2}-1)^{2}+{k}^{2}({x}_{1}-1)^{2}}$
=(1+k2)|x1x2-(x1+x2)+1|
=$\frac{9(1+{k}^{2})}{3+4{k}^{2}}$,
∴$\frac{|AF|+|BF|}{|AF|•|BF|}$=$\frac{|AB|}{|AF|•|BF|}$=$\frac{\frac{12(1+{k}^{2})}{3+4{k}^{2}}}{\frac{9(1+{k}^{2})}{3+4{k}^{2}}}$=$\frac{4}{3}$;
综上所述,|AF|+|BF|=$\frac{4}{3}$|AF|•|BF|,
即存在实数$λ=\frac{4}{3}$,使得|AF|+|BF|=λ|AF|•|BF|恒成立.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
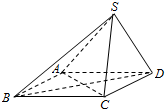 已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.
已知在四棱锥S-ABCD中,底面ABCD是平行四边形,若SB⊥AC,SA=SC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com