
分析 由已知得到a,b与p的关系,代入原函数,可得f(x)=x3-3px2+x+2p3-p,求出使函数f(x)有一个不动点的p的范围,验证存在p使函数f(x)恰有一个零点得答案.
解答 证明:∵f(x)=x3+ax2+x+b的图象关于点(p,0)对称,
设M(x,y),M关于点(p,0)的对称点为M′(2p-x,-y),
则-y=(2p-x)3+a(2p-x)2+(2p-x)+b,
即y=-(2p-x)3-a(2p-x)2-(2p-x)-b=x3-(6p+a)x2+(12p2-4ap+1)x-8p3-4ap2-2p-b,
∴$\left\{\begin{array}{l}{a=-(6p+a)}\\{b=-8{p}^{3}-4a{p}^{2}-2p-b}\end{array}\right.$,则a=-3p,b=2p3-p.
∴f(x)=x3-3px2+x+2p3-p.
由f(x)恰有一个不动点,得x3-3px2+x+2p3-p=x只有一个实根,
即x3-3px2+2p3-p=0只有一个实根,
令g(x)=x3-3px2+2p3-p,
g′(x)=3x2-6px,
∴当x∈(-∞,0),(2p,+∞)时,g′(x)>0,
当x∈(0,2p)时,g′(x)<0,
∴g(x)的极大值为g(0)=2p3-p,极小值为g(2p)=4p3-p.
要使g(x)=x3-3px2+2p3-p只有一个零点,则2p3-p<0或4p3-p>0,
解得:p>0.
由f(x)=x3-3px2+x+2p3-p.
得f′(x)=3x2-6px+1,
当△=36p2-12≤0,即-$\frac{\sqrt{3}}{3}≤p≤\frac{\sqrt{3}}{3}$时,f′(x)≥0恒成立,f(x)在R上单调递增,f(x)仅有一个零点;
∴存在P,使得f(x)恰有一个零点.
∴“f(x)恰有一个零点”是“f(x)恰有一个不动点”的充分不必要条件.
点评 本题考查必要条件、充分条件、充要条件的判定方法,训练了利用导数求函数的最值,考查学生的逻辑思维能力和推理论证能力,是中档题.


科目:高中数学 来源: 题型:解答题
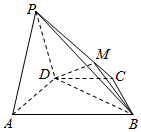 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=4,$AB=2DC=2\sqrt{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 假设a,b,c都小于0 | B. | 假设a,b,c中至少有一个不大于0 | ||
| C. | 假设a,b,c中至多有一个不小于0 | D. | 假设a,b,c中至多有一个不大于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b都大于0 | B. | a,b都小于0 | C. | a,b不都大于0 | D. | a,b都不大于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图茎叶图记录了在一次数学模拟考试中甲、乙两组各五名学生的成绩(单位:分).已知甲组数据的中位数为106,乙组数据的平均数为105.4,则x,y的值分别为( )
如图茎叶图记录了在一次数学模拟考试中甲、乙两组各五名学生的成绩(单位:分).已知甲组数据的中位数为106,乙组数据的平均数为105.4,则x,y的值分别为( )| A. | 5,7 | B. | 6,8 | C. | 6,9 | D. | 8,8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com