
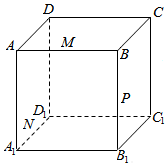
 如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.
如图所示,正方体ABCD-A1B1C1D1的棱长为8cm,M,N,P分别是AB,A1D1,BB1的中点.分析 (1)根据MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上,连接NK交BC与Q,与平面BB1C1C的交线是PQ.
(2)根据(1)得到的交线PQ,在Rt△BPQ中,由勾股定理可求得.
解答 解:(1)如图所示:∵MP?平面ABB1,
∴MP与底面ABCD的交点K必在侧面ABB1与底面ABCD的交线AB上,
∴过点M,N,P的平面与平面ABCD的交线是NK,(K在线段AB的延长线上),与平面BB1C1C的交线是PQ(Q在线段BC上).∵BK∥A1B1,
∴$\frac{BK}{{MB}_{1}}$=$\frac{BP}{{PB}_{1}}$=1,∴BK=4.
∵BQ∥AN,∴$\frac{BK}{AK}$=$\frac{BQ}{AN}$=$\frac{1}{3}$,
∴BQ=$\frac{4}{3}$.
(2)由(1)可知:BQ=$\frac{4}{3}$,BP=4,在Rt△BPQ中,由勾股定理得PQ=$\sqrt{{4}^{2}{+(\frac{4}{3})}^{2}}$=$\frac{4}{3}$$\sqrt{10}$.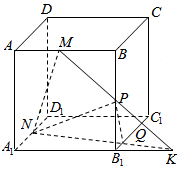
点评 本题考查了平面与平面的交线及交线长等问题,正确画出交线是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
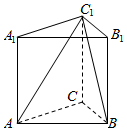 如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.
如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,AA1⊥面A1B1C1,正视图是边长为2正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
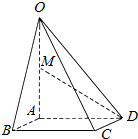 如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.
如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
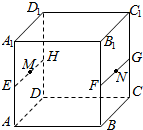 若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )
若直线a上的所有点到两条直线m、n的距离都相等,则称直线a为“m、n的等距线”.在正方体ABCD-A1B1C1D1中,E、F、G、H分别是所在棱中点,M、N分别为EH、FG中点,则在直线MN,EG,FH,B1D中,是“A1D1、AB的等距线”的条数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
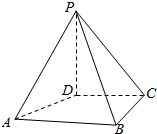 如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com