练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．已知集合A={0，1，a}，B={0，3，3a}，若A∩B={0，3}，则A∪B={0，1，3，9}．

    分析 根据集合的基本运算进行求解即可．

    解答 解：∵A∩B={0，3}，
    ∴a=3，
    则B={0，3，9}，
    则A∪B={0，1，3，9}，
    故答案为：{0，1，3，9}，

    点评 本题主要考查集合的基本运算，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    17．已知f（x）=lnx+$\frac{1}{x}$，且2＜p＜q．，求证：对于x∈（p，q），有$\frac{f（x）-f（p）}{x-p}$＞$\frac{f（x）-f（q）}{x-q}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若函数f（x）=ax3+ax2+x-1在实数R上是增函数，则实数a的取值范围是（　　）
    A．[-1，2]B．[0，3]C．[2，5]D．（0，3）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

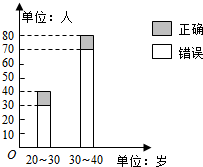    15．“开门大吉”是某电视台推出的游戏节目．选手面对1～8号8扇大门，依次按响门上的门铃，门铃会播放一段音乐（将一首经典流行歌曲以单音色旋律的方式演绎），选手需正确回答出这首歌的名字，方可获得该扇门对应的家庭梦想基金．在一次场外调查中，发现参赛选手多数分为两个年龄段：20～30；30～40（单位：岁），其猜对歌曲名称与否的人数如图所示．
    （1）写出2×2列联表；判断是否有90%的把握认为猜对歌曲名称与否和年龄有关；说明你的理由；（下面的临界值表供参考）
    P（K2≥k0）0.100.050.0100.005
    k02.7063.8416.6357.879
    （2）现计划在这次场外调查中按年龄段选取9名选手，并抽取3名幸运选手，求3名幸运选手中在20～30岁之间的人数的分布列和数学期望．
    （参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．5位同学排队，其中3位女生，2位男生．如果2位男生不能相邻，且女生甲不能排在排头，则排法种数为60．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若双曲线t2y2-x2=t2（t≠0）经过点$（2，\sqrt{2}）$，则该双曲线的离心率为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．2D．$\sqrt{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．在等腰△ABC中，角A，B，C的对边分别为a，b，c，若sinB=sinAcosC-$\frac{1}{2}$sinC，且a=$\sqrt{3}$，则△ABC的面积为（　　）
    A．$\frac{3\sqrt{3}}{4}$B．$\frac{\sqrt{3}}{4}$
    C．$\sqrt{3}$D．条件不足，无法计算

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知函数f（x）满足f（0）=1，且对于任意实数x，y∈R都有：f（xy+1）=f（x）f（y）-f（y）-x+2，若x∈[1，3]，则$\frac{f（x-1）}{{f}^{2}（x）+1}$的最大值为（　　）
    A．$\frac{\sqrt{2}-1}{2}$B．$\frac{\sqrt{2}+1}{2}$C．$\frac{1}{5}$D．$\frac{3}{17}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．已知半圆C：（x-2）2+y2=4（y≥0），直线 l：x-2y-2=0．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系．
    （I）写出C与 l的极坐标方程；
    （Ⅱ）记A为C直径的右端点，C与l交于点M，且M为圆弧AB的中点，求|OB|．

    查看答案和解析>>

    同步练习册答案