
分析 由题意可知求得直线l的方程,代入抛物线方程,点A在x轴上方,即可求得A点坐标,利用两点之间的距离公式,即可求得丨OA丨.
解答 解:抛物线y2=4x的焦点F的坐标为(1,0)
∵直线l过F,倾斜角为60°,即斜率k=tanα=$\sqrt{3}$,
∴直线l的方程为:y=$\sqrt{3}$(x-1),即x=$\frac{\sqrt{3}}{3}$y+1,
$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{3}y+1}\\{{y}^{2}=4x}\end{array}\right.$,解得:$\left\{\begin{array}{l}{y=2\sqrt{3}}\\{x=3}\end{array}\right.$,$\left\{\begin{array}{l}{y=-\frac{2\sqrt{3}}{3}}\\{x=\frac{1}{3}}\end{array}\right.$,
由点A在x轴上方,则A(3,2$\sqrt{3}$),
则|OA|=$\sqrt{(3)^{2}+(2\sqrt{3})^{2}}$=$\sqrt{21}$,
则丨OA丨=$\sqrt{21}$,
故答案为:$\sqrt{21}$.
点评 本题考查直线与抛物线的位置关系,考查直线的点斜式方程,考查计算能力,属于中档题.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {0,1} | C. | [0,2) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
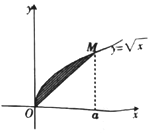 如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )
如图,点M在曲线y=$\sqrt{x}$,若由曲线y=$\sqrt{x}$与直线OM所围成的阴影部分的面积为$\frac{1}{6}$,则实数a等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -462 | B. | 462 | C. | 792 | D. | -792 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
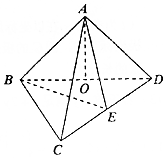 如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.
如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com