
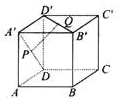
 如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明.
如图,在正方体ABCD-A′B′C′D′中,P是A′D的中点,Q是B′D′的中点,判断直线PQ与平面AA′B′B的位置关系,并利用定义证明. 分析 直线与平面的关系,转化为平面与平面的关系;P是A′D的中点,Q是B′D′的中点,作A′D′的中点为N.可得平面AA′B′B与平面PQN的关系,判断直线PQ与平面AA′B′B的位置关系.
解答 解:直线PQ与平面AA′B′B平行.
证明:∵P是A′D的中点,Q是B′D′的中点,作A′D′的中点为N.
连接PN,QN,可得:PN∥A′A,QN∥A′B′,
A′A∩A′B′=A′,PN、QN?平面PQN,A′A、A′B′?平面AA′B′B
∴平面AA′B′B与平面PQN平行.
∵PQ?平面PQN
故得直线PQ与平面AA′B′B平行.
点评 本题考查了直线与平面的关系,转化为平面与平面的关系来证明.比较基础.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-8y2 | B. | y=-8x2 | C. | x=-16y2 | D. | y=-16x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 奇偶性与k的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3≤x≤3} | B. | {x|-3≤x<0或0<x≤3} | C. | {x|x≤-3或x≥3} | D. | {x|x≤-3或x=0或x≥3} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com