练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．如图，一不规则区域内，有一边长为1米的正方形，向区域内随机地撒1000颗黄豆，数得落在正方形区域内（含边界）的黄豆数为360颗，以此实验数据1000为依据可以估计出该不规则图形的面积为$\frac{25}{9}$平方米．（用分数作答）

    分析 根据几何概型的意义进行模拟试验计算不规则图形的面积，利用面积比可得结论．

    解答 解：∵向区域内随机地撒1000颗黄豆，数得落在正方形区域内（含边界）的黄豆数为360颗，
    记“黄豆落在正方形区域内”为事件A，
    ∴P（A）=$\frac{360}{1000}$=$\frac{1}{S}$，
    ∴S不规则图形=$\frac{25}{9}$平方米，
    故答案为：$\frac{25}{9}$．

    点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．若z1=sin2θ+icosθ，z2=cosθ+i$\sqrt{3}$sinθ，当θ=$\frac{π}{6}+2kπ，k∈Z$时，z1=z2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若动点M（x，y）始终满足关系式$\sqrt{{x}^{2}+（y+2）^{2}}$+$\sqrt{{x}^{2}+（y-2）^{2}}$=8，则动点N的轨迹方程为（　　）
    A．$\frac{x^2}{16}+\frac{y^2}{12}$=1B．$\frac{x^2}{12}+\frac{y^2}{16}$=1C．$\frac{x^2}{12}-\frac{y^2}{16}$=1D．$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{12}$=1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数$f（x）=sin（2x-\frac{π}{6}）$．
    （I）求函数f（x）的最小正周期；
    （Ⅱ）求函数f（x）的单调递增区间；
    （Ⅲ）当$x∈[{0，\frac{2π}{3}}]$时，求函数f（x）的最小值，并求出使y=f（x）取得最小值时相应的x值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．抛物线y2=2px（p＞0）与直线y=x+1相切，A（x1，y1），B（x2，y2）（x1≠x2）是抛物线上两个动点，F为抛物线的焦点，且|AF|+|BF|=8．
    （Ⅰ）求p的值；
    （Ⅱ） 线段AB的垂直平分线l与x轴的交点是否为定点，若是，求出交点坐标，若不是，说明理由；
    （Ⅲ）求直线l的斜率的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数f（x）是定义在R上的奇函数，且当x＞0时，f（x）=$\frac{3}{x}$-1
    （Ⅰ）求f（0），f（-2）的值
    （Ⅱ）用函数单调性的定义证明函数f（x）在（0，+∞）上是减函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

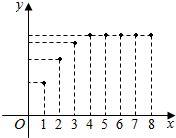    14．甲工厂八年来某种产品年产量与时间（单位：年）的函数关系如图所示．现有下列四种说法：
    ①前三年该产品产量增长速度越来越快；
    ②前三年该产品产量增长速度越来越慢；
    ③第三年后该产品停止生产；
    ④第三年后该产品年产量保持不变．
    其中说法正确的是（　　）
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知定义在R上的函数f（x），对任意的x，y∈R都有f（x+y）=f（x）+f（y），且当x＞0时，f（x）＞0．
    （Ⅰ）求f（0）的值，判断f（x）的奇偶性并说明理由；
    （Ⅱ）求证：f（x）在（-∞，+∞）上是增函数；
    （Ⅲ）若不等式f（k•2x）+f（2x-4x-2）＜0对任意x∈R恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ax2-ax-1（a∈R）．
    （1）若对任意实数x，f（x）＜0恒成立，求实数a的取值范围；
    （2）当a＞0时，解关于x的不等式f（x）＜2x-3．

    查看答案和解析>>

    同步练习册答案