
分析 (I)由题设知c=$\sqrt{3}$,$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,由此能求出椭圆C的方程.
(II)设M(x1,y1) N(x2,y2),右顶点A(2,0),由以MN为直径的圆经过椭圆C的右顶点A,知(2-x2)(2-x1)+y1y2=0,把y=x+m代入椭圆方程,再由韦达定理结合题设条件能求出直线方程.
解答 解:(1)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,a>b>0,
左焦点F(-$\sqrt{3}$,0),且离心率e=$\frac{\sqrt{3}}{2}$,∴c=$\sqrt{3}$,$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴a=2,b2=4-3=1,
∴椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}$=1.
(II)证明:设M(x1,y1) N(x2,y2),右顶点A(2,0),$\overrightarrow{AM}$=(2-x1,y1),$\overrightarrow{AN}$=(2-x2,y2),
∵以MN为直径的圆经过椭圆C的右顶点A,
∴(2-x2)(2-x1)+y1y2=0,
∵y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2
∴4+(m-2)(x1+x2)+2x1x2+m2=0 ①
把y=x+m代入椭圆方程$\frac{{x}^{2}}{4}+{y}^{2}$=1,得$\frac{{x}^{2}}{4}$+(x+m)2=1,
整理,得$\frac{5}{4}$x2+2mx+m2-1=0,
所以x1x2=$\frac{4}{5}({m}^{2}-1)$,x1+x2=-$\frac{8}{5}km$,②
把②入①,得
4+(km-2)•(-$\frac{8}{5}km$)+(1+k2)•$\frac{4}{5}({m}^{2}-1)$+m2
=(5m2+16m+12)÷(1+4)
=(m+2)(5m+6)÷(1+4)=0
所以m+2=0 或者 m+$\frac{6}{5}$=0
当m+2=0时,直线y=x-2恒过点(2,0)和A点重合显然不符合
当m+$\frac{6}{5}$=0时 直线恒过点($\frac{6}{5}$,0)符合题意
∴直线l的方程y=x-$\frac{6}{5}$.
点评 本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与双曲线的相关知识,解题时要注意合理地进行等价转化.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
已知椭圆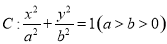 过点
过点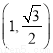 ,且离心率为
,且离心率为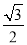 .
.
(1)求椭圆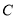 的标准方程;
的标准方程;
(2)若点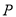 与点
与点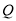 均在椭圆
均在椭圆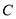 上,且
上,且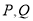 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点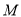 (点
(点 在一象限),使得
在一象限),使得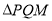 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点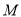 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
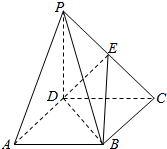 如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.
如图,已知四棱锥P-ABCD的底面是矩形,PD⊥平面ABCD,PD=CD,点E是PC的中点,连接DE、BD、BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
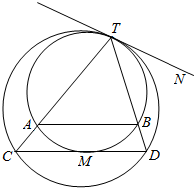 如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.
如图所示,两个圆相内切于点T,公切线为TN,外圆的弦TC,TD分别交内圆于A、B两点,并且外圆的弦CD恰切内圆于点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
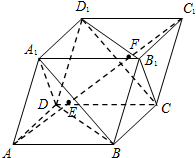 如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.
如图,已知平行六面体ABCD-A1B1C1D1中,AC1与平面A1BD、CB1D1交于点E、F两点.设K为△B1CD1的外心,则VK-BED:${V_{{A_1}-BFD}}$=$\frac{1}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com