
分析 根据题意,画出图形,结合图形,利用半径r,圆心M到点P的距离MP以及切线长组成直角三角形,即可求出弦长AB.
解答 解:如图所示,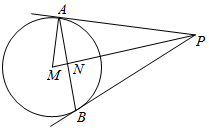
⊙M:x2+y2-4x-4y-1=0可化为(x-2)2+(y-2)2=9,
∴圆心为M(2,2),半径为r=3;
则圆心M到点P的距离为
d=MP=$\sqrt{{(5-2)}^{2}{+(5-2)}^{2}}$=3$\sqrt{2}$,
∴切线长PA=$\sqrt{{MP}^{2}{-r}^{2}}$=$\sqrt{{(3\sqrt{2})}^{2}{-3}^{2}}$=3,
∴弦AB的长为2×$\frac{PA•r}{MP}$=2×$\frac{3×3}{3\sqrt{2}}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 本题考查了直线与圆的应用问题,也考查了勾股定理的应用问题,是基础题目.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
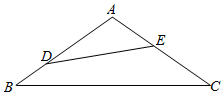 某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°
某小区要将如图所示的一块三角形边角地修建成花圃.根据建造规划,要求横穿花圃的直线灌溉水道DE恰好把花圃分成面积相等的两部分(其中D在边AB上,E在边AC上)已知AB=AC=2a,∠BAC=120°查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com