Question

4．已知：P是直线l：3x+4y+13=0的动点，PA是圆C：x²+y²-2x-2y-2=0的一条切线，A是切点，那么△PAC的面积的最小值是2$\sqrt{3}$．

Answer 1

分析 求出圆的标准方程，以及三角形的面积，将面积的最值问题转化为点到直线的距离问题是解决本题的关键．

解答 解：圆的标准方程为（x-1）²+（y-1）²=4，
则圆心坐标为C（1，1），半径R=2，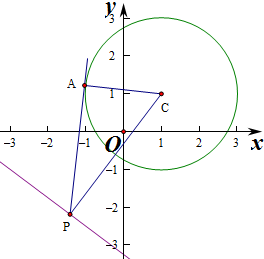
则△PAC的面积S=$\frac{1}{2}PA•AC=\frac{1}{2}×2PA=PA$，
∴要使△PAC的面积的最小，则PA最小，
即PC最小即可，此时最小值为圆心C到直线的距离d=$\frac{|3+4+13|}{\sqrt{{3}^{2}+{4}^{2}}}=\frac{20}{5}=4$，
即PC=d=4，
此时PA=$\sqrt{P{C}^{2}-A{C}^{2}}=\sqrt{16-4}=\sqrt{12}$=2$\sqrt{3}$，
即△PAC的面积的最小值为S=2$\sqrt{3}$，
故答案为：2$\sqrt{3}$

点评 本题主要考查直线和圆的位置关系的应用，将三角形的面积进行转化，以及利用数形结合是解决本题的关键．