考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)连结A
1D,交AD
1于F,连结OF,EF,由已知得OF∥AA
1∥CC
1,从而OF
CE,进而四边形OCEF为平行四边形,由此能证明OC∥平面AED
1.
(2)以O为原点,OA为x轴,OB为y轴,OA
1为z轴,建立空间直角坐标系,求出平面AED
1的法向量和平面ADD
1的法向量,利用向量法能求出二面角E-AD
1-D的余弦值.
解答:
(1)证明:连结A
1D,交AD
1于F,连结OF,EF,
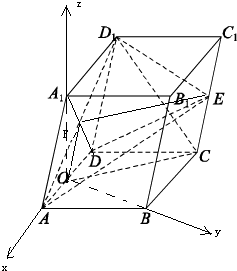
则F为A
1D的中点,也为AD
1的中点,
∵E、O分别为棱CC
1和棱AD的中点,
∴OF∥AA
1∥CC
1,且OF=
AA
1,
又∵CE=
CC
1,∴OF
CE,
∴四边形OCEF为平行四边形,∴OC∥EF,
∵EF?平面AED
1,OC?平面AED
1,
∴OC∥平面AED
1.
(2)解:∵斜四棱体ABCD-A
1B
1C
1D
1各棱长都是2,
∠BAD=∠A
1AD=60°,E、O分别是棱CC
1和棱AD的中点,
平面ADD
1A
1⊥平面ABCD,
∴以O为原点,OA为x轴,OB为y轴,OA
1为z轴,
建立空间直角坐标系,
E(-2,
,
),A(1,0,0),D
1(-1,0,
),
=(-3,
,),
=(-2,0,
),
设平面AED
1的法向量
=(x,y,z),
则
,取z=2
,得
=(3,2
,2
),
又平面ADD
1的法向量
=(0,1,0),
设二面角E-AD
1-D的平面角为θ,
cosθ=
=
=
.
∴二面角E-AD
1-D的余弦值为
.
点评:本题主要考查直线与平面之间的平行、垂直等位置关系,线线角、线面角、二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力.

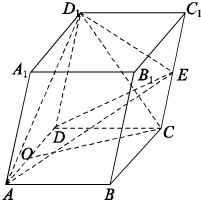 已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.
已知斜四棱体ABCD-A1B1C1D1各棱长都是2,∠BAD=∠A1AD=60°,E、O分别是棱CC1和棱AD的中点,平面ADD1A1⊥平面ABCD.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案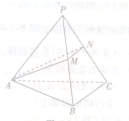 如图所示,在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、PC的中点,若平面AMN⊥平面PBC,则平面AMN与平面ABC成二面角(锐角)的余弦值等于( )
如图所示,在三棱锥P-ABC中,PA=PB=PC,底面△ABC是正三角形,M、N分别是侧棱PB、PC的中点,若平面AMN⊥平面PBC,则平面AMN与平面ABC成二面角(锐角)的余弦值等于( )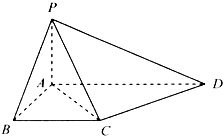 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=