Question

4．已知圆M：（x-1）²+（y-1）²=4，直线l：x+y-6=0，A为直线l上一点．
（1）若AM⊥l，过A作圆M的两条切线，切点分别为P，Q，求∠PAQ的大小；
（2）若圆M上存在两点B，C，使得∠BAC=60°，求点A横坐标的取值范围．

Answer 1

分析 （1）确定△APM是等腰直角三角形，可得∠PAM=45°，同理得∠QAM=45°，即可求∠PAQ的大小；
（2）从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，不妨设切线为AP，AQ，则∠PAQ为60°时，∠PMQ为120°，所以MA的长度为4，故可确定点A的横坐标x₀的取值范围．

解答 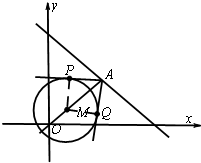解：（1）由题知AM⊥l，即AM为M点到直线l的距离，AM=2$\sqrt{2}$，…2分
在直角三角形APM中，AM=2$\sqrt{2}$，PM=2，∴AP=2
∴△APM是等腰直角三角形，…5分
∴∠PAM=45°，…6分
同理得∠QAM=45°
∴∠PAQ=90°                        …8分
（2）由题意，从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角，
不妨设切线为AP，AQ，则∠PAQ为60°时，∠PMQ为120°，所以MA的长度为4，
故问题转化为在直线上找到一点，使它到点M的距离为4．
设A（x₀，6-x₀），则
∵M（1，1），∴（x₀-1）²+（5-x₀）²=16
∴x₀=1或5
∴点A的横坐标x₀的取值范围是[1，5]…16分．

点评 本题考查直线与圆的方程的应用，考查学生分析解决问题的能力，解题的关键是明确从直线上的点向圆上的点连线成角，当且仅当两条线均为切线时才是最大的角．