
分析 (1)若f(x)为“局部奇函数”,则根据定义计算即可;
(2)根据题意:“姊妹点”,可知,欲求f(x)的“姊妹点”,只须作出函数y=x2+2x(x<0)的图象关于原点对称的图象,看它与函数y=$\frac{2}{{e}^{x}}$(x≥0)交点个数即可.
解答 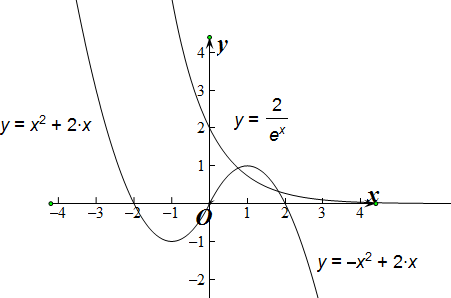 解:(1)若f(x)为“局部奇函数”等价于关于x的方程f(-x)+f(x)=0有解.
解:(1)若f(x)为“局部奇函数”等价于关于x的方程f(-x)+f(x)=0有解.
当f(x)=ax2+2x-4a时,
由f(-x)+f(x)=0得2a(x2-4)=0
解得x=±2,
(2)根据题意:“姊妹点对”,可知,
只须作出函数y=x2+2x(x<0)的图象关于原点对称的图象,
看它与函数y=$\frac{2}{{e}^{x}}$(x≥0)交点个数即可.如图,
观察图象可得:它们的交点个数是:2.
即f(x)的“姊妹点对”有:2个.
故答案为:±2,2.
点评 本题主要考查与函数奇偶性有关的新定义,合理地利用图象法解决,根据条件建立方程关系是解决本题的关键,考查学生的计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C,D是⊙O上的点,AD是∠BAC的平分线,过点D作DE⊥AC,交AC的延长线于点E.
如图,AB是⊙O的直径,C,D是⊙O上的点,AD是∠BAC的平分线,过点D作DE⊥AC,交AC的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
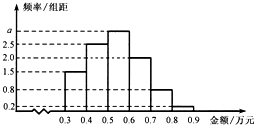 某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.
某电子商务公司对10000名网络购物者2014年度的消费情况进行统计,发现消费金额(单位:万元)都在区间[0.3,0.9]内,其频率分布直方图如图所示.直方图中的a=3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
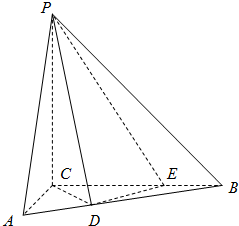 三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4
三棱锥P-ABC中,PC⊥平面ABC,PC=6,BC⊥AC,D,E分别是线段AB.BC上的点,且CD=DE=2$\sqrt{2}$,CE=2EB=4查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{sin0.5}$ | B. | sin0.5 | C. | 2sin1 | D. | $\frac{1}{cos0.5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com