
分析 (Ⅰ)由题意,f′(x)=$\frac{a+1}{\sqrt{x}}$,利用直线y=x+1是函数y=f(x)图象的一条切线,建立方程,即可求a的值;
(Ⅱ)①记h(x)=f(x)-g(x),则h(x)=2$\sqrt{x}$-lnx-bx(x>0),由题意,令h′(x)=$\frac{-bx+\sqrt{x}-1}{x}$=0可得bx-$\sqrt{x}$+1=0,方程有两个正数根,即可试求b的取值范围;
②求出$\frac{g({x}_{1})+g({x}_{2})}{f({x}_{1})+f({x}_{2})}$=$\frac{1}{2}$-blnb-b,再求最值,即可证明结论.
解答 (Ⅰ)解:由题意,f′(x)=$\frac{a+1}{\sqrt{x}}$.
设直线y=x+1与函数y=f(x)图象的切点为(x0,y0),
∴$\left\{\begin{array}{l}{{y}_{0}=2(a+1)\sqrt{{x}_{0}}}\\{{y}_{0}={x}_{0}+1}\\{\frac{a+1}{\sqrt{{x}_{0}}}=1}\end{array}\right.$,∴a=0,x0=1,y0=2;
(Ⅱ)解:①记h(x)=f(x)-g(x),则h(x)=2$\sqrt{x}$-lnx-bx(x>0),
∴h′(x)=$\frac{-bx+\sqrt{x}-1}{x}$
由题意,令h′(x)=$\frac{-bx+\sqrt{x}-1}{x}$=0可得bx-$\sqrt{x}$+1=0,方程有两个正数根
设t=$\sqrt{x}$,则$\left\{\begin{array}{l}{1-4b>0}\\{\frac{1}{b}>0}\end{array}\right.$,∴0<b<$\frac{1}{4}$.
∴0<b<$\frac{1}{4}$时,函数y=f(x)-g(x)在其定义域有两个极值点;
②证明:设bx-$\sqrt{x}$+1=0的两个根为x1,x2.则x1x2=$\frac{1}{{b}^{2}}$,x1+x2=$\frac{1}{{b}^{2}}$-$\frac{2}{b}$,
∵g(x1)+g(x2)=lnx1+bx1+lnx2+bx2=ln(x1x2)+b(x1+x2)
∴g(x1)+g(x2)=-2lnb+b($\frac{1}{{b}^{2}}$-$\frac{2}{b}$)=-2lnb+$\frac{1}{b}$-2
∵f(x1)+f(x2)=2$\sqrt{{x}_{1}}$+2$\sqrt{{x}_{2}}$=$\frac{2}{b}$,
∴$\frac{g({x}_{1})+g({x}_{2})}{f({x}_{1})+f({x}_{2})}$=$\frac{1}{2}$-blnb-b
记k(b)=$\frac{1}{2}$-blnb-b(0<b<$\frac{1}{4}$),则k′(b)=-lnb-2=0,可得b=$\frac{1}{{e}^{2}}$,
(0,$\frac{1}{{e}^{2}}$)时,k′(b)>0,函数单调递增,($\frac{1}{{e}^{2}}$,$\frac{1}{4}$)时,k′(b)<0,函数单调递减,
∴b=$\frac{1}{{e}^{2}}$时,k(b)取得最大值$\frac{1}{{e}^{2}}$+$\frac{1}{2}$,
∴$\frac{g({x}_{1})+g({x}_{2})}{f({x}_{1})+f({x}_{2})}$≤$\frac{1}{{e}^{2}}$+$\frac{1}{2}$.
点评 本题考查导数知识的综合运用,考查导数的几何意义,考查函数的最值,正确求导,确定函数的单调性是关键.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-2$\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
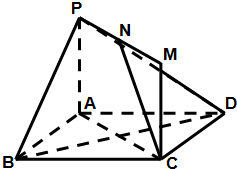 如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,
如图,矩形ACMP和菱形ABCD所在的平面互相垂直,点N为PM的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱∠DOT=2∠DMB中,已知∠BMC=30°.,AB=BC=1,BB1=2,$∠BC{C_1}=\frac{π}{3}$.
如图,在三棱柱∠DOT=2∠DMB中,已知∠BMC=30°.,AB=BC=1,BB1=2,$∠BC{C_1}=\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com