
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 和
和![]() 的中点,且
的中点,且![]() .
.
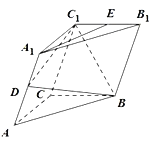
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)先根据![]() 且
且![]() ,
,![]() 且
且![]() 可知四边形
可知四边形![]() 为平行四边形,由此
为平行四边形,由此![]() ,进而得证;
,进而得证;
(2)先证明![]() 平面
平面![]() ,由此可以
,由此可以![]() 为坐标原点,射线
为坐标原点,射线![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正半轴,以平行于
轴的正半轴,以平行于![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 与平面
与平面![]() 的法向量,再利用向量的夹角公式得解.
的法向量,再利用向量的夹角公式得解.
(1)如图![]() ,取线段
,取线段![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
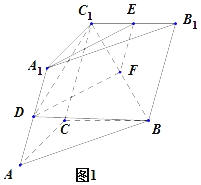
![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,
又![]() 为
为![]() 的中点,
的中点,![]() 且
且![]() ,
,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)作![]() 于点
于点![]() ,由
,由![]() ,得
,得![]() ,
,
![]() ,即
,即![]() 为
为![]() 的中点,
的中点,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,从而有
,从而有![]() ,
,
又![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
故可以点![]() 为坐标原点,射线
为坐标原点,射线![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正半轴,以平行于
轴的正半轴,以平行于![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系,如图
轴,建立空间直角坐标系,如图![]() ,
,
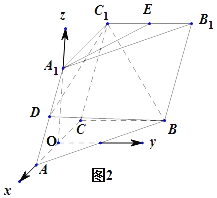
令![]() ,则
,则![]() 、
、![]() 、
、![]() 、
、![]() 、
、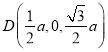 ,
,
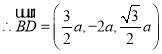 ,
,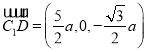 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则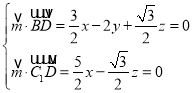 ,
,
取![]() ,则
,则![]() ,
,![]() ,可得
,可得![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,则
,则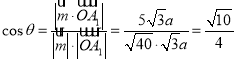 ,
,
因此,平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为4.且过点
的焦距为4.且过点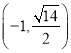 .
.
(1)求椭圆E的方程;
(2)设![]() ,
,![]() ,
,![]() ,过B点且斜率为
,过B点且斜率为![]() 的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线
的直线l交椭圆E于另一点M,交x轴于点Q,直线AM与直线![]() 相交于点P.证明:
相交于点P.证明:![]() (O为坐标原点).
(O为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了提高生产线的运行效率,工厂对生产线的设备进行了技术改造.为了对比技术改造后的效果,采集了生产线的技术改造前后各![]() 次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
次连续正常运行的时间长度(单位:天)数据,并绘制了如茎叶图:
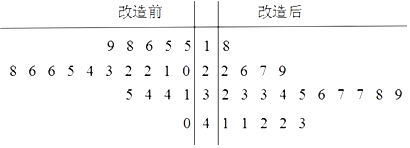
(1)①设所采集的![]() 个连续正常运行时间的中位数
个连续正常运行时间的中位数![]() ,并将连续正常运行时间超过
,并将连续正常运行时间超过![]() 和不超过
和不超过![]() 的次数填入下面的列联表:
的次数填入下面的列联表:
超过 | 不超过 | |
改造前 |
|
|
改造后 |
|
|
②根据①中的列联表,能否有![]() 的把握认为生产线技术改造前后的连续正常运行时间有差异?
的把握认为生产线技术改造前后的连续正常运行时间有差异?
附: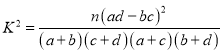 .
.
|
|
|
|
|
|
|
|
(2)工厂的生产线的运行需要进行维护,工厂对生产线的生产维护费用包括正常维护费、保障维护费两种.对生产线设定维护周期为![]() 天(即从开工运行到第
天(即从开工运行到第![]() 天
天![]() 进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为
进行维护.生产线在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产线能连续运行,则不会产生保障维护费;若生产线不能连续运行,则产生保障维护费.经测算,正常维护费为![]() 万元/次;保障维护费第一次为
万元/次;保障维护费第一次为![]() 万元/周期,此后每增加一次则保障维护费增加
万元/周期,此后每增加一次则保障维护费增加![]() 万元.现制定生产线一个生产周期(以
万元.现制定生产线一个生产周期(以![]() 天计)内的维护方案:
天计)内的维护方案:![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() .以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
.以生产线在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往统计资料,某地车主购买甲种保险的概率为0.4,购买乙种保险但不购买甲种保险的概率为0.2.设各车主购买保险相互独立.
(1)求该地1位车主至少购买甲乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲乙两种保险都不购买的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )
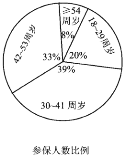
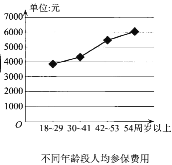
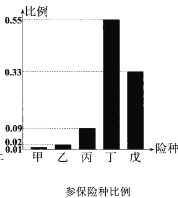
A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)在函数![]() 的图象上取
的图象上取![]() 两个不同的点,令直线
两个不同的点,令直线![]() 的斜率为
的斜率为![]() ,则在函数的图象上是否存在点
,则在函数的图象上是否存在点![]() ,且
,且![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 两点的坐标,若不存在,说明理由.
两点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有某种不透明充气包装的袋装零食,每袋零食附赠玩具A,B,C中的一个.对某零售店售出的100袋零食中附赠的玩具类型进行追踪调查,得到以下数据:
BBABC ACABA AAABC BABAA CAAAB
ABCCC BCBBC CABCA BACAB BCBCB
BCCCA BCCAA BCCCB ACCBB BACAB
ACCAB BBBAA CABCA BCBBC CABCA
(1)能否认为购买一袋该零食,获得玩具A,B,C的概率相同?请说明理由;
(2)假设每袋零食随机附赠玩具A,B,C是等可能的,某人一次性购买该零食3袋,求他能从这3袋零食中集齐玩具A,B及C的概率![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com