
分析 (Ⅰ)由$\left\{\begin{array}{l}ρ=2cosθ\\ ρ=sinθ\end{array}\right.$,得2cosθ=sinθ,化简即可得出kOA.
(Ⅱ)设A的极角为θ,tanθ=2,则$sinθ=\frac{{2\sqrt{5}}}{5},cosθ=\frac{{\sqrt{5}}}{5}$,把$B({{ρ_1},θ-\frac{π}{2}})$,代入ρ=2cosθ得ρ1.把$C({{ρ_2},θ+\frac{π}{2}})$,代入ρ=sinθ得ρ2,利用|BC|=ρ1+ρ2,即可得出.
解答 解:(Ⅰ)由$\left\{\begin{array}{l}ρ=2cosθ\\ ρ=sinθ\end{array}\right.$,得2cosθ=sinθ,tanθ=2,∴kOA=2.
(Ⅱ)设A的极角为θ,tanθ=2,则$sinθ=\frac{{2\sqrt{5}}}{5},cosθ=\frac{{\sqrt{5}}}{5}$,
则$B({{ρ_1},θ-\frac{π}{2}})$,代入ρ=2cosθ得${ρ_1}=2cos({θ-\frac{π}{2}})=2sinθ=\frac{{4\sqrt{5}}}{5}$.
$C({{ρ_2},θ+\frac{π}{2}})$,代入ρ=sinθ得${ρ_2}=sin({θ+\frac{π}{2}})=cosθ=\frac{{\sqrt{5}}}{5}$,
∴$|{BC}|={ρ_1}+{ρ_2}=\frac{{4\sqrt{5}}}{5}+\frac{{\sqrt{5}}}{5}=\sqrt{5}$.
点评 本题考查了极坐标方程的应用、斜率计算、弦长计算,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\overrightarrow{AB}+\overrightarrow{CD})+\overrightarrow{BC}$ | B. | $(\overrightarrow{AD}+\overrightarrow{MB})+(\overrightarrow{BC}+\overrightarrow{CM})$ | C. | $\overrightarrow{OC}-\overrightarrow{OA}+\overrightarrow{CD}$ | D. | $\overrightarrow{MB}+\overrightarrow{AD}-\overrightarrow{BM}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
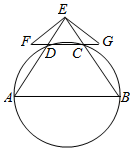 如图,A,B,C,D四点在同一圆上,AB∥CD,AD的延长线与BC的延长线交于E点.
如图,A,B,C,D四点在同一圆上,AB∥CD,AD的延长线与BC的延长线交于E点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
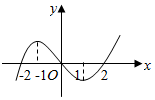
| A. | (-∞,-1)∪(0,1) | B. | (-1,0)∪(1,+∞) | C. | (-2,-1)∪(1,2) | D. | (-∞,-2)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com