【题目】已知A、B、C为△ABC的三个内角，且其对边分别为a、b、c，若cosBcosC﹣sinBsinC= 
．
（1）求角A；
（2）若a=2 
，b+c=4，求△ABC的面积．
【答案】
（1）解：在△ABC中，∵cosBcosC﹣sinBsinC= 
，
∴cos（B+C）= ，
又∵0＜B+C＜π，
∴B+C= 
，
∵A+B+C=π，
∴A= 
（2）解：由余弦定理a2=b2+c2﹣2bccosA，
得（2 
）2=（b+c）2﹣2bc﹣2bccos ，
把b+c=4代入得：12=16﹣2bc+bc，
整理得：bc=4，
则△ABC的面积S= bcsinA= ×4× 
=
【解析】（1）已知等式左边利用两角和与差的余弦函数公式化简，求出cos（B+C）的值，确定出B+C的度数，即可求出A的度数；（2）利用余弦定理列出关系式，再利用完全平方公式变形，将a与b+c的值代入求出bc的值，再由sinA的值，利用三角形面积公式即可求出三角形ABC面积．
浙江名校名师金卷系列答案科目：高中数学 来源： 题型：
【题目】如图，在棱长为2的正方体
中， 
， 
， 
， 
分别是棱
， 
， 
， 
的中点，点
， 
分别在棱
， 
上移动，且
.
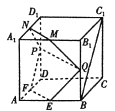
（1）当
时，证明：直线
平面
；
（2）是否存在
，使面
与面
所成的二面角为直二面角？若存在，求出
的值；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】山西某公司有一批专业技术人员，对他们进行年龄状况和接受教育程度（本科学历）的调查，其结果（人数分布）如表：
学历 | 35岁以下 | 35 | 50岁以上 |
本科 | 80 | 30 | 20 |
研究生 |
| 20 |
|
（Ⅰ）用分层抽样的方法在
岁年龄段的专业技术人员中抽取一个容量为10的样本，将该样本看成一个总体，从中任取3人，求至少有1人的学历为研究生的概率；
（Ⅱ）在这个公司的专业技术人员中按年龄状况用分层抽样的方法抽取
个人，其中35岁以下48人，50岁以上10人，再从这个人中随机抽取出1人，此人的年龄为50岁以上的概率为
，求
、
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
， 
（
为常数）.
（1）函数
的图象在点
处的切线与函数
的图象相切，求实数
的值；
（2）若函数
在定义域上存在单调减区间，求实数
的取值范围；
（3）若
， 
，且
，都有
成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和为Sn ， 若4Sn=（2n﹣1）an+1+1，且a1=1．
（1）求数列{an}的通项公式；
（2）设cn= 
，数列{cn}的前n项和为Tn ．
①求Tn；
②对于任意的n∈N*及x∈R，不等式kx2﹣6kx+k+7+3Tn＞0恒成立，求实数k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
的参数方程为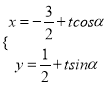
（
为参数），以
为极点， 
轴的非负半轴为极轴，建立极坐标系，曲线
的极坐标方程为
，（ 
）
（1）写出直线
经过的定点的直角坐标，并求曲线
的普通方程；
（2）若
，求直线
的极坐标方程，以及直线
与曲线
的交点的极坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB，证明： 
（1）CD=BC；
（2）△BCD∽△GBD．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
