Question

4．美团外卖和百度外卖两家公司其“骑手”的日工资方案如下：美团外卖规定底薪70元，每单抽成1元；百度外卖规定底薪100元，每日前45单无抽成，超出45单的部分每单抽成6元，假设同一公司的“骑手”一日送餐单数相同，现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数，得到如下条形图：

（Ⅰ）求百度外卖公司的“骑手”一日工资y（单位：元）与送餐单数n的函数关系；
（Ⅱ）若将频率视为概率，回答下列问题：
①记百度外卖的“骑手”日工资为X（单位：元），求X的分布列和数学期望；
②小明拟到这两家公司中的一家应聘“骑手”的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．

Answer 1

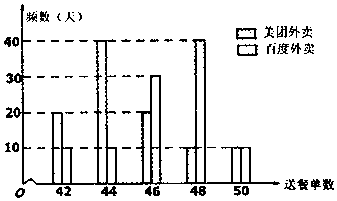
分析 （Ⅰ）当送餐单数n≤45，n∈N^*时，百度外卖公司的“骑手”一日工资y=100，当送餐单数n＞45，n∈N^*时，百度外卖公司的“骑手”一日工资y=100+（n-45）×6=6n-170，n∈N^*，由此能求出百度外卖公司的“骑手”一日工资y（单位：元）与送餐单数n的函数关系．
（Ⅱ）①记百度外卖的“骑手”日工资为X（单位：元），由条形图得X的可能取值为100，106，118，130，分别求出相应的概率，由此能求出X的分布列和E（X）．
②先求出美团外卖“骑手”日平均送餐单数，再求出美团外卖“骑手”日平均工资和百度外卖“骑手”日平均工资为112元．由此推荐小明去美团外卖应聘．

解答 解：（Ⅰ）∵百度外卖规定底薪100元，每日前45单无抽成，超出45单的部分每单抽成6元，
∴当送餐单数n≤45，n∈N^*时，百度外卖公司的“骑手”一日工资y=100，
当送餐单数n＞45，n∈N^*时，百度外卖公司的“骑手”一日工资y=100+（n-45）×6=6n-170，n∈N^*，
∴百度外卖公司的“骑手”一日工资y（单位：元）与送餐单数n的函数关系为：
$y=\left\{{\begin{array}{l}{100（n≤45，n∈{N^*}）}\\{6n-170（n＞45，n∈{N^*}）}\end{array}}\right.$
（Ⅱ）①记百度外卖的“骑手”日工资为X（单位：元），由条形图得X的可能取值为100，106，118，130，
P（X=100）=$\frac{10+10}{100}$=0.2，
P（X=106）=$\frac{30}{100}$=0.3，
P（X=118）=$\frac{40}{100}$=0.4，
P（X=130）=$\frac{10}{100}$=0.1，
∴X的分布列为：

X	100	106	118	130
P	0.2	0.3	0.4	0.1

E（X）=100×0.2+106×0.3+118×0.4+130×0.1=112（元）．
②美团外卖“骑手”日平均送餐单数为：42×0.2+44×0.4+46×0.2+48×0.1+50×0.1=45
所以美团外卖“骑手”日平均工资为：70+45×1=115（元）
由①知，百度外卖“骑手”日平均工资为112元．
故推荐小明去美团外卖应聘．

点评 本题考查条形图的应用，考查离散型随机的分布列和数学期望的求法，考查数据处理能力、运算求解能力以及应用意识，考查必然与或然思想等，是基础题．