
分析 由题意建立直角坐标系,取$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),从而可得$\overrightarrow{c}$=(1,1),|$\overrightarrow{c}$|=$\sqrt{2}$;从而可得|$\overrightarrow{c}$+t$\overrightarrow{a}$+$\frac{1}{t}$$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{c}}^{2}+{t}^{2}{\overrightarrow{a}}^{2}+\frac{1}{{t}^{2}}{\overrightarrow{b}}^{2}+2t\overrightarrow{a}•\overrightarrow{c}+\frac{2}{t}\overrightarrow{b}•\overrightarrow{c}+2\overrightarrow{a}•\overrightarrow{b}}$
=$\sqrt{2+2(t+\frac{1}{t})+{t}^{2}+\frac{1}{{t}^{2}}}$≥$\sqrt{2+4+2}$=2$\sqrt{2}$.
解答  解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{c}$•$\overrightarrow{a}$=$\overrightarrow{c}$•$\overrightarrow{b}$=1,
解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,$\overrightarrow{c}$•$\overrightarrow{a}$=$\overrightarrow{c}$•$\overrightarrow{b}$=1,
建立如图所示的直角坐标系,取$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),
设$\overrightarrow{c}$=(x,y),
∴(x,y)•(1,0)=(x,y)•(0,1)=1.
∴x=y=1.
∴$\overrightarrow{c}$=(1,1),
∴|$\overrightarrow{c}$|=$\sqrt{2}$;
∵t>0.
∴|$\overrightarrow{c}$+t$\overrightarrow{a}$+$\frac{1}{t}$$\overrightarrow{b}$|=$\sqrt{{\overrightarrow{c}}^{2}+{t}^{2}{\overrightarrow{a}}^{2}+\frac{1}{{t}^{2}}{\overrightarrow{b}}^{2}+2t\overrightarrow{a}•\overrightarrow{c}+\frac{2}{t}\overrightarrow{b}•\overrightarrow{c}+2\overrightarrow{a}•\overrightarrow{b}}$
=$\sqrt{2+2(t+\frac{1}{t})+{t}^{2}+\frac{1}{{t}^{2}}}$≥$\sqrt{2+4+2}$=2$\sqrt{2}$,
当且仅当t=1时取等号.
故答案为:2$\sqrt{2}$.
点评 本题考查了平面向量应用及基本不等式在求最值中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
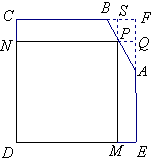 有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2.
有一块铁皮零件,其形状是由边长为40cm的正方形截去一个三角形ABF所得的五边形ABCDE,其中AF=12cm,BF=10cm,如图所示.现在需要用这块材料截取矩形铁皮DMPN,使得矩形相邻两边分别落在CD,DE上,另一顶点P落在边CB或BA边上.设DM=xcm,矩形DMPN的面积为ycm2. 查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.
执行如图所示的程序框图,输出的结果为a,二项式${({\sqrt{m}{x^2}+\frac{1}{{\sqrt{x}}}})^4}$的展开式中x3项的系数为$\frac{a}{2}$,则常数m=$\frac{1}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com