
分析 根据函数的关系式,求出数列{an}的通项公式,判断数列是等比数列,求出它的前n项和Sn.
解答 解:令y=x,f(x)•f(x)=f(2x),
∴f(2x)=[f(x)]2,x∈R;
又a1=$\frac{1}{2}$,an=f(n)(n∈N*),
∴a1=f(1)=$\frac{1}{2}$,
an=f(n)=[f(1)]n=${(\frac{1}{2})}^{n}$;
∴数列{an}是首项为a1=$\frac{1}{2}$,公比q=$\frac{1}{2}$的等比数列,
其前n项和为Sn=$\frac{\frac{1}{2}(1{-(\frac{1}{2})}^{n})}{1-\frac{1}{2}}$=$1-{(\frac{1}{2})^n}$.
故答案为:1-${(\frac{1}{2})}^{n}$.
点评 本题考查了函数的性质与应用问题,也考查了等比数列的定义与通项公式、前n项和公式的应用问题,是综合性题目.


科目:高中数学 来源: 题型:选择题
| A. | 4x-3y-19=0 | B. | 4x+3y-13=0 | C. | 3x-4y-16=0 | D. | 3x+4y-8=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
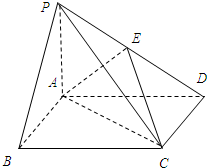 在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,
在如图所示四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是正方式,PA=AB=1,E是PD上的点,PB∥平面AEC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com