
分析 设A(x1,y1),B(x2,y2),则x=1+$\frac{\sqrt{3}}{3}$y代入y2=4x得:y2-$\frac{3\sqrt{3}}{3}$y-4=0,S=$\frac{1}{2}$|OF|•|y1-y2|,由此能求出△OAB的面积.
解答 解:设A(x1,y1),B(x2,y2),则
过F且倾斜角为60°的直线y=$\sqrt{3}$(x-1),
即x=1+$\frac{\sqrt{3}}{3}$y代入y2=4x得:y2-$\frac{3\sqrt{3}}{3}$y-4=0,∴y1+y2=$\frac{{4\sqrt{3}}}{3}$,y1y2=-4,
∴|y1-y2|=$\sqrt{\frac{48}{9}+16}$=$\frac{8\sqrt{3}}{3}$,
∴S=$\frac{1}{2}$|OF|•|y1-y2|=$\frac{1}{2}$×1×$\frac{8\sqrt{3}}{3}$=$\frac{{4\sqrt{3}}}{3}$.
故答案为$\frac{{4\sqrt{3}}}{3}$.
点评 本题主要考查了抛物线的简单性质,直线与抛物线的位置关系.在涉及焦点弦的问题时常需要把直线与抛物线方程联立利用韦达定理设而不求,进而利用抛物线的定义求得问题的答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1)∪(2,+∞) | B. | (-∞,-2)∪(1,+∞) | C. | (1,2) | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 1 | B. | $\sqrt{2015}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2017}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{33}{65}$或$\frac{63}{65}$ | B. | $\frac{63}{65}$ | C. | $\frac{33}{65}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
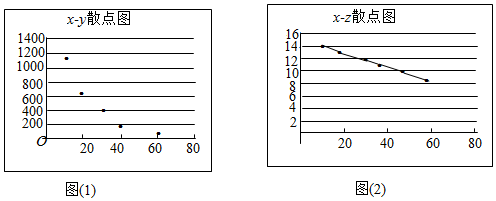
| 定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
| 年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
| z=2lny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\frac{\sqrt{3}-1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{1}{3}$) | B. | (-3,-1) | C. | (-1,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,若P处有一棵树与两墙的距离分别是4m和am(0<a<12),不考虑树的粗细.现用16m长的篱笆,借助墙角围成一个矩形花圃ABCD.设此矩形花圃的最大面积为u,若将这棵树围在矩形花圃内,则函数u=f(a)(单位m2)的图象大致是( )| A. |  | B. | 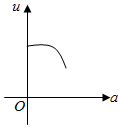 | C. | 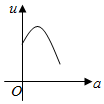 | D. | 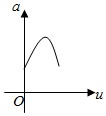 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com