
 如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.
如图所示,在四棱柱ABCD-A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1.分析 (Ⅰ)通过已知条件易得$|\overrightarrow{AB}|$=$|\overrightarrow{A{A}_{1}}|$、∠DAB=∠DAA1,利用$\overrightarrow{{A}_{1}B}•\overrightarrow{AD}$=0即得A1B⊥AD;
(Ⅱ)通过建立空间直角坐标系O-xyz,平面DCC1D1与平面ABB1A1所成锐二面角的余弦值即为平面ABB1A1的法向量与平面DCC1D1的一个法向量的夹角的余弦值,计算即可.
解答 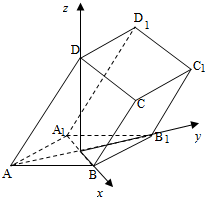 (Ⅰ)通过条件可知$|\overrightarrow{AB}|$=$|\overrightarrow{A{A}_{1}}|$、∠DAB=∠DAA1,利用$\overrightarrow{{A}_{1}B}•\overrightarrow{AD}$=即得A1B⊥AD;
(Ⅰ)通过条件可知$|\overrightarrow{AB}|$=$|\overrightarrow{A{A}_{1}}|$、∠DAB=∠DAA1,利用$\overrightarrow{{A}_{1}B}•\overrightarrow{AD}$=即得A1B⊥AD;
(Ⅱ)解:设线段A1B的中点为O,连接DO、AB1,
由题意知DO⊥平面ABB1A1.
因为侧面ABB1A1为菱形,所以AB1⊥A1B,
故可分别以射线OB、射线OB1、射线OD为x轴、y轴、z轴
的正方向建立空间直角坐标系O-xyz,如图所示.
设AD=AB=2BC=2a,由∠A1AB=60°可知|0B|=a,$|OA|=|O{B}_{1}|=\sqrt{3}a$,
所以$|OD|=\sqrt{|AD{|}^{2}-|OA{|}^{2}}$=a,从而A(0,$-\sqrt{3}$a,0),B(a,0,0),
B1(0,$\sqrt{3}$a,0),D(0,0,a),所以$\overrightarrow{C{C}_{1}}$=$\overrightarrow{B{B}_{1}}$=(-a,$\sqrt{3}$a,0).
由$\overrightarrow{BC}=\frac{1}{2}\overrightarrow{AD}$可得C(a,$\frac{\sqrt{3}}{2}$a,$\frac{1}{2}$a),所以$\overrightarrow{DC}$=(a,$\frac{\sqrt{3}}{2}$a,-$\frac{1}{2}$a),
设平面DCC1D1的一个法向量为$\overrightarrow{m}$=(x0,y0,z0),
由$\overrightarrow{m}$•$\overrightarrow{C{C}_{1}}$=$\overrightarrow{m}$•$\overrightarrow{DC}$=0,得$\left\{\begin{array}{l}{-a{x}_{0}+\sqrt{3}a{y}_{0}=0}\\{a{x}_{0}+\frac{\sqrt{3}}{2}a{y}_{0}-\frac{1}{2}a{z}_{0}=0}\end{array}\right.$,
取y0=1,则x0=$\sqrt{3}$,z0=$3\sqrt{3}$,所以$\overrightarrow{m}$=($\sqrt{3}$,1,$3\sqrt{3}$).
又平面ABB1A1的法向量为$\overrightarrow{OD}$=D(0,0,a),
所以$cos<\overrightarrow{OD},\overrightarrow{m}>$=$\frac{\overrightarrow{OD}•\overrightarrow{m}}{|\overrightarrow{OD}||\overrightarrow{m}|}$=$\frac{3\sqrt{3}a}{\sqrt{31}a}$=$\frac{3}{31}\sqrt{93}$,
故平面DCC1D1与平面ABB1A1所成锐二面角的余弦值为$\frac{3}{31}\sqrt{93}$.
点评 本题考查二面角,空间中两直线的位置关系,向量数量积运算,注意解题方法的积累,建立坐标系是解决本题的关键,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD、PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=∠CDA=90°,PA⊥平面ABCD,PA=AD=AB=2,CD=1,M,N分别是PD、PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 在正方形ABCD-A1B1C1D1中,Q是CC1的中点,F是侧面BCB1C1内的动点且A1F∥平面D1AQ,则A1F与平面BCB1C1所成角的正切值得取值范围为[2,2$\sqrt{2}$].
在正方形ABCD-A1B1C1D1中,Q是CC1的中点,F是侧面BCB1C1内的动点且A1F∥平面D1AQ,则A1F与平面BCB1C1所成角的正切值得取值范围为[2,2$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…、第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=3,S3=$\frac{17}{4}$.
把公差为2的等差数列{an}的各项依次插入等比数列{bn}的第1项、第2项、…、第n项后,得到数列{cn}:b1,a1,b2,a2,b3,a3,b4,a4,…,记数列{cn}的前n项和为Sn,已知c1=1,c2=3,S3=$\frac{17}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{5}$,1] | B. | [$\frac{1}{6}$,$\frac{5}{4}$] | C. | [$\frac{1}{6}$,$\frac{3}{2}$] | D. | [$\frac{1}{5}$,$\frac{5}{4}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com