
| A. | f(x)=x2+2x | B. | f(x)=cosx | C. | f(x)=2x-1 | D. | f(x)=$\frac{1}{2}$(ex-e-x) |
分析 根据条件分别进行验证,依次进行判断即可.
解答 解:A.∵f($\frac{{x}_{1}+{x}_{2}}{2}$)-$\frac{f({x}_{1})+f({x}_{2})}{2}$=($\frac{{x}_{1}+{x}_{2}}{2}$)2+2×($\frac{{x}_{1}+{x}_{2}}{2}$)-$\frac{1}{2}$x12-x1-$\frac{1}{2}$x22-x2=-$\frac{({x}_{1}-{x}_{2})^{2}}{4}$<0恒成立,
即f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;成立,满足条件.
B.f(x)=cosx的图象不满足条件.比如当x1=0,x2=$\frac{π}{2}$时,f($\frac{{x}_{1}+{x}_{2}}{2}$)=f($\frac{π}{4}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{1}{2}$(0+1)=$\frac{1}{2}$,不满足条件f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$.
C.f(x)=2x-1为单调函数,不满足条件.
D.f(x)=$\frac{1}{2}$(ex-e-x)为单调函数,不满足条件.
故选:A
点评 本题主要考查抽象函数的应用,根据定义转化为进行判断或者使用排除法是解决本题的关键.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:选择题
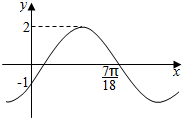
| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 296 | B. | 221 | C. | 225 | D. | 641 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com