
已知函数
(1)判断函数 的奇偶性;
的奇偶性;
(2)试用函数单调性定义说明函数 在区间
在区间 和
和 上的增减性;
上的增减性;
(3)若 满足:
满足: ,试证明:
,试证明: .
.
(1)偶函数,(2)在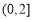 上是减函数,在
上是减函数,在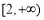 上是增函数(3)详见解析.
上是增函数(3)详见解析.
【解析】
试题分析:(1)判定函数奇偶性,首先判定函数定义域是否关于原点对称,然后再判断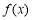 与
与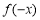 的相等或相反关系.本题定义域为一切实数,关于原点对称.函数
的相等或相反关系.本题定义域为一切实数,关于原点对称.函数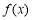 为分段函数,需分类讨论. 当
为分段函数,需分类讨论. 当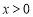 时,
时,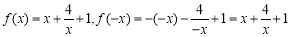 ,
,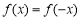 .当
.当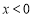 时,
时,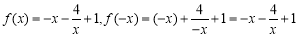 ,
,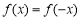 .故
.故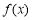 为偶函数.(2)利用定义研究函数单调性,需注重作差后的变形,关键是提取公因式,进行因式分解,以便判断符号.(3)由于
为偶函数.(2)利用定义研究函数单调性,需注重作差后的变形,关键是提取公因式,进行因式分解,以便判断符号.(3)由于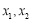 是同区间的两个任意数,所以只需证
是同区间的两个任意数,所以只需证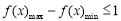 ,从而本题实质为求函数最值.由函数奇偶性及单调性知:
,从而本题实质为求函数最值.由函数奇偶性及单调性知:
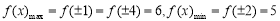 ,所以
,所以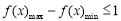 成立.
成立.
试题解析:【解析】
(1)∵当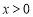 时,
时,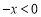 ,∴
,∴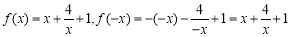
∴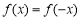 2分
2分
∵当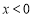 时,
时,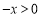 ,∴
,∴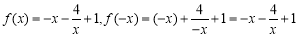
∴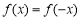 4分
4分
∴对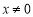 都有
都有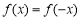 ,故
,故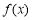 为偶函数 5分
为偶函数 5分
(2)当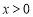 时,
时,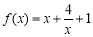
设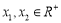 且
且 ,则
,则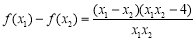 7分
7分
∴当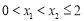 时,
时,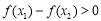 即
即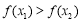
当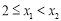 时,
时, 即
即 9分
9分
∴函数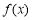 在区间
在区间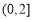 上是减函数,在区间
上是减函数,在区间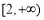 上是增函数 11分
上是增函数 11分
(3)由(2)可知,当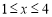 时:
时:
若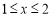 ,则
,则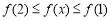 即
即
若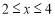 ,则
,则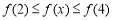 即
即
∴当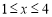 时,有
时,有 12分
12分
又由(1)可知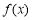 为偶函数,∴当
为偶函数,∴当 时,有
时,有 13分
13分
∴若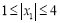 ,
,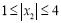 时,则
时,则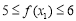 ,
,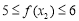 14分
14分
∴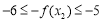 ,
,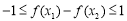 即
即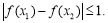 15分
15分
考点:分段函数的奇偶性、单调性.


科目:高中数学 来源:2015届浙江省高三上学期第一次统练文科数学试卷(解析版) 题型:填空题
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r=;类比这个结论可知:四面体S ?ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为R,四面体S ?ABC的体积为V,则R= .
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高三上学期第一次统练文科数学试卷(解析版) 题型:选择题
将函数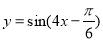 图象上各点的横坐标伸长到原来的2倍,再向左平移
图象上各点的横坐标伸长到原来的2倍,再向左平移 个单位,
个单位,
纵坐标不变,所得函数图象的一条对称轴的方程是( )
(A)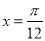 (B)
(B)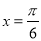 (C)
(C)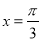 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2015届浙江省高二下学期第一次质量检测数学试卷(解析版) 题型:填空题
下图展示了一个由区间(0,1)到实数集R的映射过程:区间(0,1)中的实数 对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在
对应数轴上的点M(点A对应实数0,点B对应实数1),如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在 轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与
轴上,点A的坐标为(0,1),在图形变化过程中,图①中线段AM的长度对应于图③中的弧ADM的长度,如图③,图③中直线AM与 轴交于点N(
轴交于点N( ),则
),则 的象就是
的象就是 ,记作
,记作

给出下列命题:① ; ②
; ② ; ③
; ③ 是奇函数; ④
是奇函数; ④ 在定义域上单调递增,则所有真命题的序号是______________.(填出所有真命题的序号)
在定义域上单调递增,则所有真命题的序号是______________.(填出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源:2015届河南长葛第三实验高中高二下学期第一次考试理数学卷(解析版) 题型:填空题
黑白两种颜色的正六形地面砖块按如图的规律拼成若干个图案,则第4个图案中有白色地面砖________________块.
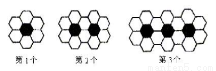
查看答案和解析>>
科目:高中数学 来源:2015届河南省濮阳市高二下学期升级考试理科试卷(A卷)(解析版) 题型:解答题
已知等差数列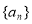 的前
的前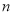 项和为
项和为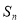 ,
,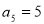 ,
, ,
,
(1)求数列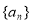 的通项公式;
的通项公式;
(2)若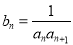 ,求数列
,求数列 的前100项和.
的前100项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com