
分析 联立方程组可得交点坐标,由夹角公式可得所求直线的斜率,可得直线的点斜式方程,化为一般式可得.
解答 解:联立方程组可得$\left\{\begin{array}{l}{3x+4y+1=0}\\{5x+12y-1=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=-1}\\{y=\frac{1}{2}}\end{array}\right.$,即两直线的交点为(-1,$\frac{1}{2}$),
又可得直线l1和l2的斜率分别为k1=$-\frac{3}{4}$,k2=$-\frac{5}{12}$,
设所求直线的斜率为k,则$|\frac{-\frac{3}{4}-k}{1-\frac{3}{4}k}|$=$|\frac{-\frac{5}{12}-k}{1-\frac{5}{12}k}|$,
当$\frac{-\frac{3}{4}-k}{1-\frac{3}{4}k}$=$\frac{-\frac{5}{12}-k}{1-\frac{5}{12}k}$时,方程可化为k2+1=0无实数解;
当$\frac{-\frac{3}{4}-k}{1-\frac{3}{4}k}$=-$\frac{-\frac{5}{12}-k}{1-\frac{5}{12}k}$时,方程可化为28k2-33k-28=0,
分解因式可得(4k-7)(7k+4)=0,解得k=$\frac{7}{4}$或k=$-\frac{4}{7}$,
当k=$\frac{7}{4}$时,可得直线的方程为y-$\frac{1}{2}$=$\frac{7}{4}$(x+1)即7x-4y+9=0;
当k=-$\frac{4}{7}$时,可得直线的方程为y-$\frac{1}{2}$=-$\frac{4}{7}$(x+1)即8x+14y+1=0.
故答案为:7x-4y+9=0或8x+14y+1=0
点评 本题考查两直线的夹角公式,涉及分类讨论的思想,属中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
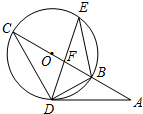 如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的
如图,AD切圆O于D点,圆O的割线ABC过O点,BC交DE于F点,若BO=2,AD=2$\sqrt{3}$.则给出的| A. | AB=2 | B. | $\frac{BF}{DF}$=$\frac{EF}{CF}$ | C. | ∠E=30° | D. | △EBD∽△CDB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com