
分析 (x+2y-$\frac{1}{z}$)6展表示6个因式(x+2y-$\frac{1}{z}$)的乘积,故其中1个因式取x,2个因式取2y,剩下的3个因式取-$\frac{1}{z}$,可得展开式中含$\frac{x{y}^{2}}{{z}^{3}}$的项,根据乘法原理求得展开式中$\frac{x{y}^{2}}{{z}^{3}}$的系数.
解答 解:∵(x+2y-$\frac{1}{z}$)6展表示6个因式(x+2y-$\frac{1}{z}$)的乘积,
故其中1个因式取x,2个因式取2y,剩下的3个因式取-$\frac{1}{z}$,
可得展开式中含$\frac{x{y}^{2}}{{z}^{3}}$的项,
故展开式中$\frac{x{y}^{2}}{{z}^{3}}$的系数为${C}_{6}^{1}$•${C}_{5}^{2}$•22•(-1)=-240,
故答案为:-240.
点评 本题主要考查乘方的意义,乘法原理的运用,考查学生的计算能力,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{y}^{2}}{6}$-$\frac{{x}^{2}}{8}$=1 | B. | $\frac{{y}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{8}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $-\frac{3}{2}$ | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{16}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
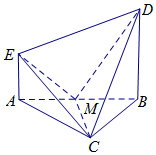 如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.
如图,EA⊥平面ABC,DB⊥平面ABC,△ABC是等边三角形,AC=2AE,M是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com