
分析 (1)运用向量垂直的条件:数量积为0,以及平方法,向量的平方即为模的平方,化简整理即可得证;
(2)△ABC的形状为等边三角形.由平方法,运用向量的平方即为模的平方,以及向量的数量积的定义和夹角,即可得到结论.
解答 解:(1)证明:由$\overrightarrow{OA}⊥\overrightarrow{OB}$,可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
由m$\overrightarrow{OA}$+n$\overrightarrow{OB}$=$\overrightarrow{OC}$,
两边平方可得m2$\overrightarrow{OA}$2+n2$\overrightarrow{OB}$2+2mn$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{OC}$2,
由A,B,C在半径为1的圆上,可得:
m2+n2=1;
(2)△ABC的形状为等边三角形.
当m=n=-1,即有$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,
即有$\overrightarrow{OA}$+$\overrightarrow{OB}$=-$\overrightarrow{OC}$,
两边平方可得,$\overrightarrow{OA}$2+$\overrightarrow{OB}$2+2$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\overrightarrow{OC}$2,
即为$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$=1•1•cos∠AOB,
可得∠AOB=120°,
同理可得∠BOC=120°,∠COA=120°,
即有△ABC的内角均为60°,
则△ABC的形状为等边三角形.
点评 本题考查向量的数量积的定义和性质,主要考查向量的平方即为模的平方,考查三角形的形状的判断,注意运用平方法,考查运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(n)中共有n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| B. | f(n)中共有n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | |
| C. | f(n)中共有n2-n项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$ | |
| D. | f(n)中共有n2-n+1项,当n=2时,f(2)=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
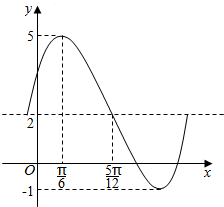 已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.
已知函数f(x)=Asin(ωx+φ)+b(A>0,ω>0,0<φ<π,b为常数)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-ln2}{2}$ | B. | $\frac{ln2}{2}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{2-2ln2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com