练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，AB为圆O的直径，PA为圆O的切线，PB与圆O相交于D，若PA＝3，PDDB＝916，则PD＝________，AB＝________.


    ，4

    [解析]　由于PDDB＝916，设PD＝9a，则DB＝16a，根据切割线定理有PA2＝PD·PB有a＝，所以PD＝，在直角△PBA中，AB2＝PB2－AP2＝16，所以AB＝4.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设计算法计算1＋2＋3＋…＋50的值时，如果用循环语句应用________语句，循环次数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，椭圆的中心在坐标原点，F为左焦点，A，B分别为长轴和短轴上的一个顶点，当FB⊥AB时，此类椭圆称为“黄金椭圆”．类比“黄金椭圆”，可推出“黄金双曲线”的离心率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    用数学归纳法证明“当n为正奇数时，xn＋yn能被x＋y整除”，当第二步假设n＝2k－1(k∈N＋)命题为真时，进而需证n＝________时，命题亦真．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    由下列不等式：1>，1＋＋>1,1＋＋＋…＋>，1＋＋＋…＋>2，…，你能得到一个怎样的一般不等式？并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC＝4，BE＝10，且BC＝AD，则DE＝(　　)

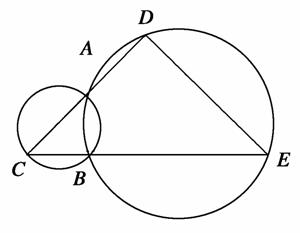
    A．6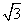                                                       B．6 

    C．8                                                             D．6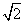

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB为⊙O的直径，直线CD与⊙O相切于E，AD垂直CD于D，BC垂直CD于C，EF垂直AB于F，连接AE，BE.证明：

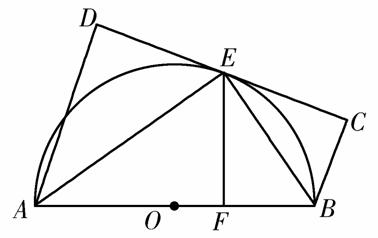
    (1)∠FEB＝∠CEB；

    (2)EF2＝AD·BC.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系xOy中，直线l的参数方程为(t为参数)，曲线C的参数方程为

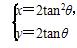    (θ为参数)．试求直线l和曲线C的普通方程，并求出它们的公共点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设m是常数，若点F(0,5)是双曲线－＝1的一个焦点，则m＝________.

    查看答案和解析>>

    同步练习册答案