
分析 (1)设抛物线方程为x2=2py(p>0),代入M(2,1),可得p=2,即可求抛物线C的方程;
(2)由|OP|=|OQ|,得$x_p^2+y_p^2=x_Q^2+y_Q^2$,即(yp-yQ)(yp+yQ+4)=0,确定∠POy=30°,${y_p}=\sqrt{3}{x_p}$,代入$x_p^2=4{y_p}$,得${x_p}=4\sqrt{3}$.即可求该等边三角形的面积;
(3)确定直线AB的方程,利用k1k2=-2,得出x1x2=-2(x1+x2)-36,由线系方程得答案.
解答 解:(1)设抛物线C 的方程为x2=2py(p>0),
由点M(2,1)在抛物线C 上,得4=2p,则p=2.
∴抛物线C 的方程为x2=4y.
(2)设该等边三角形OPQ 的顶点P,Q 在抛物线上,且P(xp,yp),Q(xQ,yQ),
则$x_p^2=4{y_p}$,$x_Q^2=4{y_Q}$,
由|OP|=|OQ|,得$x_p^2+y_p^2=x_Q^2+y_Q^2$,即(yp-yQ)(yp+yQ+4)=0.
又yp>0,yQ>0,则yp=yQ,|xp|=|xQ|,即线段PQ 关于y 轴对称.
∴∠POy=30°,${y_p}=\sqrt{3}{x_p}$,代入$x_p^2=4{y_p}$,得${x_p}=4\sqrt{3}$.
∴该等边三角形边长为$8\sqrt{3}$,${S_{△POQ}}=48\sqrt{3}$.
(3)设A(x1,y1),B(x2,y2),则$x_1^2=4{y_1}$,$x_2^2=4{y_2}$,
∴${k_1}{k_2}=\frac{{{y_1}-1}}{{{x_1}-2}}•\frac{{{y_2}-1}}{{{x_2}-2}}=\frac{{\frac{1}{4}x_1^2-1}}{{{x_1}-2}}•\frac{{\frac{1}{4}x_2^2-1}}{{{x_2}-2}}=\frac{1}{16}({x_1}+2)({x_2}+2)=-2$.
∴x1x2=-2(x1+x2)-36 ①
又${k_{AB}}=\frac{{{y_2}-{y_1}}}{{{x_2}-{x_1}}}=\frac{{\frac{1}{4}x_2^2-\frac{1}{4}x_1^2}}{{{x_2}-{x_1}}}=\frac{1}{4}({x_1}+{x_2})$,
∴直线AB 方程为:$y-{y_1}=\frac{{{x_1}+{x_2}}}{4}(x-{x_1})$,
代入①,化简得:$y-9=\frac{{{x_1}+{x_2}}}{4}(x+2)$,
所以直线AB 恒过定点(-2,9).
点评 本题考查轨迹方程,考查了直线与圆锥曲线的关系,考查了学生的计算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
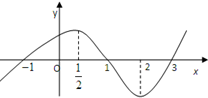
| A. | (-∞,0)∪($\frac{1}{2}$,1) | B. | (-∞,0)∪(1,2) | C. | (-∞,$\frac{1}{2}$)∪(1,2) | D. | (-∞,$\frac{1}{2}$)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,5) | B. | (-1,5] | C. | (-1,2) | D. | (-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com