
分析 由已知得cosα>0,由此利用同角三角函数关系式能求出结果.
解答 解:∵sinα•tanα=$\frac{si{n}^{2}α}{cosα}$>0,∴cosα>0,
∴$\sqrt{\frac{1-sinα}{1+sinα}}$-$\sqrt{\frac{1+sinα}{1-sinα}}$=$\sqrt{\frac{(1-sinα)^{2}}{1-si{n}^{2}α}}$-$\sqrt{\frac{(1+sinα)^{2}}{1-si{n}^{2}α}}$
=$\sqrt{\frac{(1-sinα)^{2}}{co{s}^{2}α}}$-$\sqrt{\frac{(1+sinα)^{2}}{co{s}^{2}α}}$
=$\frac{1-sinα}{cosα}-\frac{1+sinα}{cosα}$
=-2×$\frac{sinα}{cosα}$
=-2tanα.
故答案为:-2tanα.
点评 本题考查三角函数值化简求值,是基础题,解题时要认真审题,注意同角三角函数关系式的合理运用.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
| A. | m≤n | B. | m<n | C. | m≥n | D. | m>n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
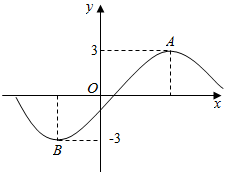 已知函数f(x)=3sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,A、B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数图象关于y轴对称,则t的最小值为6.
已知函数f(x)=3sin(ωx+φ)(ω>0,|φ|≤$\frac{π}{2}$)的部分图象如图所示,A、B两点之间的距离为10,且f(2)=0,若将函数f(x)的图象向右平移t(t>0)个单位长度后所得函数图象关于y轴对称,则t的最小值为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
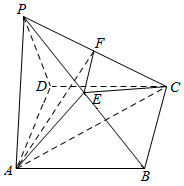 如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.
如图,四棱锥P-ABCD中,底面四边形ABCD是正方形,PA=AB=1,PA⊥平面ABCD,E为棱PB上一点,PD∥平面ACE,过E作PC的垂线,垂足为F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com