
分析 (1)问题转化为|x-2|+|x-1|-x-1>0,设函数y=|x-2|+|x-1|-x-1,通过讨论x的范围求出不等式的解集即可;
(2)问题 等价于|2k-1|≤2,解出即可.
解答 解(1)k=1时,不等式f(x)>g(x)化为:|x-2|+|x-1|-x-1>0,
设函数y=|x-2|+|x-1|-x-1,则y=$\left\{\begin{array}{l}{2-3x,x<1}\\{-x,1≤x≤2}\\{x-4,x>2}\end{array}\right.$,
令y>0,解得:x>4或x<$\frac{2}{3}$,
∴原不等式的解集是{x|x<$\frac{2}{3}$或x>4};
(2)∵f(x)-|kx-1|+|kx-2k|>|kx-1-kx+2k|-|2k-1|,
∴存在x0∈R,使得不等式f(x0)≤2成立
等价于|2k-1|≤2,解得:-$\frac{1}{2}$≤k≤$\frac{3}{2}$,
故所求实数k的范围是[-$\frac{1}{2}$,$\frac{3}{2}$].
点评 本题考查了绝对值不等式问题,考查函数恒成立问题以及分类讨论思想,是一道中档题.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 1,$\frac{π}{2}$ | B. | 1,-$\frac{π}{2}$ | C. | 3,$\frac{π}{6}$ | D. | 3,-$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(π-2x) | B. | y=sin2xcos2x | C. | y=cos22x+1 | D. | y=cos(2x-π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
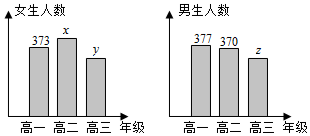
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com