
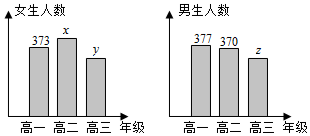
分析 (1)根据题意,有全校共有学生2000名,其中高二年级女生x名,且抽到高二年级女生的概率是0.19,结合频率、频数和样本容量之间的关系,可得,(2)根据高二男女生一起750人,又高一学生750人,所以高三男女生一起500人,按分层抽样,做出高三年级应抽取的人数;
(3)根据所给的条件列举出所有的情况,可得其情况数目,同时可得女生比男生多的情况数目,由等可能事件的概率公式,计算可得答案.
解答 解:(1)根据题意,全校共有学生2000名,其中高二年级女生x名,
且抽到高二年级女生的概率是0.19,则有$\frac{x}{2000}$=0.19,
∴x=380;
(2)由图可得,高二男生有370人,则高二男女生一起750人,高一学生750人,
所以高三男女生共2000-750-750=500人,
按分层抽样,高三年级应抽取$\frac{60}{2000}$×500=15人;
(3)因为y+z=500,y≥245,z≥245,所以基本事件有:
y=245,z=255;y=246,z=254;y=247,z=253;y=248,z=252;y=249,z=251;y=250,z=250;
y=251,z=249;y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245;一共11个基本事件.
其中女生比男生多,即y>z的基本事件有:
y=251,z=249,y=252,z=248;y=253,z=247;y=254,z=246;y=255,z=245
共5个基本事件,
故女生必男生多的事件的概率为$\frac{5}{11}$
点评 本题考查古典概型计算与频率直方图的使用,关键是正确使用频率分步直方图,其次是在列举所有的事件时,做到不重不漏.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
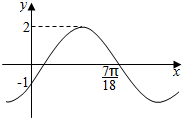
| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数 | B. | f(x)在R上单调递增 | C. | f(x)的值域为R | D. | f(x)是周期函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com