
分析 (1)设出切线方程,利用$\overrightarrow{OM}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,表示出$\overrightarrow{OM}$,求出模长,利用基本不等式即可求得结论;
(2)设点D(x0,y0),点C(x1,y1)(y1≠±y0),写出直线直线CD、CE的方程,利用方程求出直线与x轴的交点坐标,计算st的值即可.
解答 解:(1)∵⊙O的方程为x2+y2=4,
设切线l的方程为$\frac{x}{a}$+$\frac{y}{b}$=1(a>0,b>0),即bx+ay-ab=0,
则A(a,0),B(0,b),
∵$\overrightarrow{OM}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$,∴$\overrightarrow{OM}$=(a,b),
∴|$\overrightarrow{OM}$|=$\sqrt{{a}^{2}{+b}^{2}}$;
又直线l与圆C相切,∴d=r,
即$\frac{|-ab|}{\sqrt{{a}^{2}{+b}^{2}}}$=2,
∴ab=2$\sqrt{{a}^{2}{+b}^{2}}$;
又ab≤$\frac{{a}^{2}{+b}^{2}}{2}$,
∴2$\sqrt{{a}^{2}{+b}^{2}}$≤$\frac{{a}^{2}{+b}^{2}}{2}$,
∴$\sqrt{{a}^{2}{+b}^{2}}$≥4,
即|$\overrightarrow{OM}$|≥4,当且仅当a=b=2$\sqrt{2}$时“=”成立;
∴|$\overrightarrow{OM}$|的最小值是4;
(2)如图所示,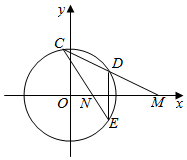
设点D(x0,y0),由对称性知点E(x0,-y0),且${{x}_{0}}^{2}$+${{y}_{0}}^{2}$=4,
设C(x1,y1)(y1≠±y0),则${{x}_{1}}^{2}$+${{y}_{1}}^{2}$=4;
所以直线CD的方程为y-y1=$\frac{{y}_{1}{-y}_{0}}{{x}_{1}{-x}_{0}}$(x-x1),
直线CE的方程为y-y1=$\frac{{y}_{1}{+y}_{0}}{{x}_{1}{-x}_{0}}$(x-x1);
在上述直线方程中,分别令y=0,
解得xM=$\frac{{{x}_{0}y}_{1}{{-x}_{1}y}_{0}}{{y}_{1}{-y}_{0}}$,xN=$\frac{{{x}_{0}y}_{1}{{+x}_{1}y}_{0}}{{y}_{1}{+y}_{0}}$,
所以st=xM•xN=$\frac{{{{(x}_{0}y}_{1})}^{2}{-{{(x}_{1}y}_{0})}^{2}}{{{y}_{1}}^{2}{{-y}_{0}}^{2}}$=$\frac{(4{{-y}_{0}}^{2}{{)y}_{1}}^{2}-(4{{-y}_{1}}^{2}{{)y}_{0}}^{2}}{{{y}_{1}}^{2}{{-y}_{0}}^{2}}$=4,
即证st为定值.
点评 本题考查了圆的切线性质与基本不等式的应用问题,也考查了平面向量以及直线斜率的应用问题,是综合性题目.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
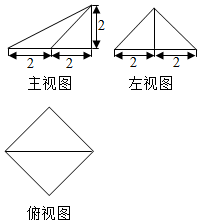
| A. | 4 | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
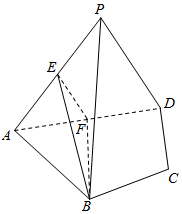 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证:
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com