考点:数列与不等式的综合,等比数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由f′(x)=a
n+2-a
n+1-(a
n-a
n+1)cosx-a
nsinx,得2a
n+1=a
n+a
n+2,由a
l、a
2、a
5成等比数列,得d=2,由此能求出a
n=2n-1.
(Ⅱ)S
n=
=n
2,b
n=
,
<
=
-
,由此能证明T
n<2.
解答:
解:(Ⅰ)∵f( x)=(a
n+2-a
n+1)x-(a
n-a
n-1)sinx+a
ncosx,
∴f′(x)=a
n+2-a
n+1-(a
n-a
n+1)cosx-a
nsinx,
∴f′(π)=a
n+2-a
n+1+a
n-a
n+1=0,即2a
n+1=a
n+a
n+2,
∴{a
n}是以a
1=1为首项的等差数列,
设数列{a
n}的公差为d,则d>0,
由a
l、a
2、a
5成等比数列,得(a
1+d)
2=a
1(a
1+4d),解得d=2,
∴a
n=2n-1.(6分)
(Ⅱ)由(Ⅰ)可得S
n=
=n
2,∴b
n=
,∴T
1=b
1=1<2.
∵当n≥2时,
<
=
-
,
∴T
n=b
1+b
2+b
3+…+b
n=
+
+
…+
<
+
+
+…+
=1+1-
+…+
-
=2-
<2,
∴T
n<2.(13分)
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.



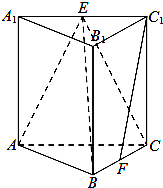 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,A1B1⊥BC,BC=1,