
已知{an}是正数组成的数列,a1=1,且点(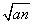 ,an+1)(n∈N+)在函数y=x2+1的图像上.
,an+1)(n∈N+)在函数y=x2+1的图像上.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=1,bn+1=bn+2an,求证:bn·bn+2<b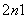 .
.
科目:高中数学 来源: 题型:
读程序回答问题
甲 乙
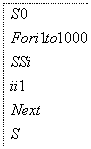

对甲、乙两程序和输出结果判断正确的是( )
A.程序不同,结果不同
B.程序不同,结果相同
C.程序相同,结果不同
D.程序相同,结果相同
查看答案和解析>>
科目:高中数学 来源: 题型:
已知x>0,由不等式x+ ≥2
≥2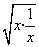 =2,x+
=2,x+ =
=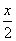 +
+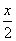 +
+ ≥3
≥3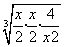 =3,…,我们可以得出推广结论:x+
=3,…,我们可以得出推广结论:x+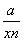 ≥n+1(n∈N+),则a=( )
≥n+1(n∈N+),则a=( )
A.2n B.n2
C.3n D.nn
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com