
分析 (1)有女生但人数必须少于男生,先取后排即可;
(2)某女生一定要担任语文科代表,除去该女生后先取后排即可;
(3)先取后排,但先安排该男生;
(4)根据题意,用间接法,先计算从12人中任选5人的选法数目,再分别计算①没有女学生入选,②只有1名女生入选,在总数中将其排除即可得答案.
解答 解:(1)先取后排,有C53C32+C54C31种,后排有A55种,共有(C53C32+C54C31)A55=5400种.….(3分)
(2)除去该女生后先取后排:C74A44=840种.…..(6分)
(3)先取后排,但先安排该男生:C74C41A44=3360种.…..(9分)
(4)根据题意,从12人中任选5人,有C105种选法,
没有女学生入选,即全选男生的情况有C75种情况,
只有1名女生入选,即选取1女4男,有C51×C74种选法,
故所有符合条件选法数为:C105-C75-C51×C74=596种,
点评 排列组合问题在实际问题中的应用,在计算时要求做到,兼顾所有的条件,先排约束条件多的元素,做的不重不漏,注意实际问题本身的限制条件.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 22 | C. | 24 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
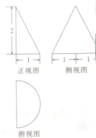
| A. | π | B. | 2+$\frac{1+\sqrt{5}}{2}π$ | C. | 2+$\frac{2+\sqrt{5}}{2}$π | D. | 2+$\frac{1}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com