
分析 (1)化f(x)为sinx的二次函数,设sinx=t,则函数g(t)是开口向下,
对称轴为t=$\frac{a}{2}$的抛物线,根据二次函数的性质,对a讨论求出函数最大值;
(2)由M(a)=2求出对应的a值即可.
解答 解:(1)f(x)=cos2x+asinx-$\frac{a}{4}$-$\frac{1}{2}$
=(1-sin2x)+asinx-$\frac{a}{4}$-$\frac{1}{2}$
=-sin2x+asinx+$\frac{2-a}{4}$,
∵0≤x≤$\frac{π}{2}$,∴0≤sinx≤1;
设sinx=t,则
g(t)=-t2+at+$\frac{2-a}{4}$,t∈[0,1];
∴f(x)的最大值为
M(a)=$\left\{\begin{array}{l}{\frac{3}{4}a-\frac{1}{2},a≥2}\\{{\frac{1}{4}a}^{2}-\frac{1}{4}a+\frac{1}{2},0<a<2}\end{array}\right.$;
(2)当M(a)=2时,
若a≥2,则$\frac{3}{4}$a-$\frac{1}{2}$=2,解得a=$\frac{10}{3}$;
若0<a<2,则$\frac{1}{4}$a2-$\frac{1}{4}$a+$\frac{1}{2}$=2,
解得a=-2或a=3,不合题意,舍去;
综上,a的值是$\frac{10}{3}$.
点评 本题主要考查了三角函数恒等变换的应用和二次函数的性质问题,是中档题.


科目:高中数学 来源: 题型:解答题
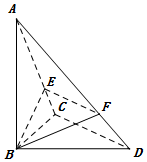 在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.
在三棱锥A-BCD中,AB⊥平面BCD,∠BCD=90°,E、F分别是AC、AD上的点,且$\frac{AE}{AC}=\frac{AF}{AD}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-2) | B. | (-1,2) | C. | (-2,1) | D. | (2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | [0,4] | C. | [3,4) | D. | (-1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 48种 | B. | 72种 | C. | 96种 | D. | 108种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com