Question

设函数f（x）=

1-|x-1|，x∈(-∞，2) 1 2 f(x-2)，x∈[2，+∞)

，则F（x）=x•[f（x）+

3

10

]-

13

10

在（0，+∞）上的零点个数为（　　）

• A、4
• B、5
• C、6
• D、7

Answer 1

考点：分段函数的应用

专题：计算题,函数的性质及应用

分析：由分段函数求出2≤x＜4时，4≤x＜6时，函数的表达式，令F（x）=0，即f（x）=

1.3

x

-0.3，画出y=f（x）的图象和y=

1.3

x

-0.3的图象，由图象观察，和零点存在定理，即可确定交点个数，即零点的个数．

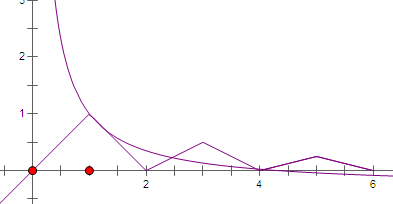
解答： 解：当x＜2时，f（x）=1-|x-1|，
当2≤x＜4时，f（x）=

1

2

f（x-2）=

1

2

（1-|x-3|）；
得4≤x＜6时，f（x）=

1

2

f（x-2）=

1

4

（1-|x-5|），
…
由于F（x）=x•[f（x）+

3

10

]-

13

10

，令F（x）=0，
即f（x）=

1.3

x

-0.3，画出y=f（x）的图象和y=

1.3

x

-0.3的图象，
由图象观察得，x＞0，一个交点为（1，1），
F（2）=2•[f（2）+0.3]-1.3＜0，F（1.25）=1.25（f（1.25）+0.3）-1.3＞0，
故还有一个交点在（1，25，2）之间，
很显然在（2，3）有一个交点，
当x=4时，f（4）=0，F（4）=4（f（4）+0.3）-1.3＜0，F（5）＞0，F（3）＞0，
即在（3，4），（4，5）内各有一个交点，
以后f（x）的图象恒在上方，故共有5个交点，
即有5个零点．
故选：B．

点评：本题考查函数的零点个数转化为方程有解问题，从而运用图象找交点问题，注意运用零点存在定理，属于中档题．