
分析 (Ⅰ)利用向量的数量积以及两角和与差的三角函数化简函数的解析式,然后求解函数f(x)的最小正周期以及单调递增区间;
(Ⅱ)利用函数的对称性以及函数的周期求解即可.
解答 (本题满分12分)
解:(I)∵向量$\overrightarrow{a}$=(2cos2x,$\sqrt{3}$),$\overrightarrow{b}$=(1,sin2x),
f(x)=$\overrightarrow{a}•\overrightarrow{b}$-1=$2{cos^2}x+\sqrt{3}sin2x-1$…(1分)
=$cos2x+\sqrt{3}sin2x$=$2sin(2x+\frac{π}{6})$,…(3分)
∴$T=\frac{2π}{2}=π$;…(4分)
由-$\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{π}{2}+2kπ$,k∈Z,
得$-\frac{π}{3}+kπ≤x≤\frac{π}{6}+kπ$,k∈Z.
所以,f(x)的单调增区间为:[-$\frac{π}{3}+kπ$,$\frac{π}{6}$+kπ],k∈Z. (7分)
(II) 由方程f(x)=k,(0<k<2),得$sin(2x+\frac{π}{6})=\frac{k}{2}$.
∵$sin(2x+\frac{π}{6})$的周期T=π,又$\frac{23π}{12}-(-\frac{π}{12})=2π$,
∴$sin(2x+\frac{π}{6})$在$[-\frac{π}{12},\frac{23π}{12}]$内有2个周期.…(9分)
∵$0<\frac{k}{2}<1$,
∴方程$sin(2x+\frac{π}{6})=\frac{k}{2}$在$[-\frac{π}{12},\frac{23π}{12}]$内有4个实根,…(10分)
且${x_1}+{x_2}=\frac{π}{3}$,${x_3}+{x_4}=\frac{7π}{3}$,…(11分)
∴所有实数根之和:x1+x2+x3+x4+x5+x6=$\frac{8π}{3}$.…(12分)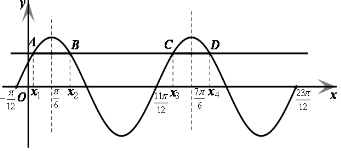
点评 本题考查两角和与差的三角函数,向量的数量积以及函数的周期,函数与方程的根的关系,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

| 成绩性别 | 优秀 | 不优秀 | 总计 |
| 男生 | |||
| 女生 | |||
| 总计 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com