
| A. | (-∞,2] | B. | (-∞,$\frac{5}{2}$] | C. | [2,$\frac{5}{2}$] | D. | [$\frac{5}{2}$,+∞) |
分析 求出函数的导数,得到函数的单调性,问题转化为a≤x+$\frac{1}{x}$在(0,2]恒成立,求出a的范围即可.
解答 解:f′(x)=$\frac{{-x}^{2}+ax-1}{{x}^{2}}$,
若不等式mf(m)+nf(n)<nf(m)+mf(n)在(0,2]恒成立,
则(m-n)[f(m)-f(n)]<0在(0,2]恒成立,
故f(x)在(0,2]递减,
故-x2+ax-1≤0在(0,2]恒成立,
故a≤x+$\frac{1}{x}$在(0,2]恒成立,
而y=x+$\frac{1}{x}$≥2在(0,2]恒成立,当且仅当x=1时取最小值2,
故a≤2,
故选:A.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想,是一道中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
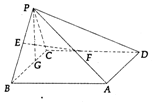 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-11)∪(4,+∞) | B. | (-11,4) | C. | (-4,-3) | D. | (-∞,-4]∪[-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,2] | B. | [$\sqrt{2}$,+∞) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16π}{3}$ | B. | $\frac{32π}{3}$ | C. | $\frac{64π}{3}$ | D. | $\frac{128π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C${\;}_{6}^{2}$A${\;}_{5}^{5}$ | B. | 5C${\;}_{6}^{1}$A${\;}_{5}^{5}$ | C. | 5A${\;}_{5}^{5}$ | D. | C${\;}_{6}^{1}$A${\;}_{5}^{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com