Question

3£®ÒÑÖªµãA£¨1£¬$\frac{{\sqrt{2}}}{2}$£©ÊÇÀëÐÄÂÊΪ$\frac{{\sqrt{2}}}{2}$£¬ÍÖÔ²C£º$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1£¨a£¾b£¾0£©ÉϵÄÒ»µã£¬Ð±ÂÊΪ$\frac{{\sqrt{2}}}{2}$µÄÖ±ÏßBD½»ÍÖÔ²CÓÚB£¬DÁ½µã£¬ÇÒA£¬B£¬DÈýµã²»Öغϣ®
£¨1£©ÇóÍÖÔ²CµÄ·½³Ì£»
£¨2£©¡÷ABDµÄÃæ»ýÊÇ·ñ´æÔÚ×î´óÖµ£¬Èô´æÔÚ£¬Çó³öÕâ¸ö×î´óÖµ£®

Answer 1

·ÖÎö £¨1£©¸ù¾ÝµãµãA£¨1£¬$\frac{{\sqrt{2}}}{2}$£©ÊÇÀëÐÄÂÊΪ$\frac{{\sqrt{2}}}{2}$µÄÍÖÔ²CÉϵÄÒ»µã£¬½¨Á¢·½³Ì£¬¼´¿ÉÇóÍÖÔ²CµÄ·½³Ì£»
£¨2£©Ö±Ïß·½³Ì´úÈëÍÖÔ²·½³Ì£¬¼ÆËã³öÈý½ÇÐεÄÃæ»ýµÄ±í´ïʽ£¬ÀûÓöþ´Îº¯ÊýµÄ×îÖµ£¬¿ÉµÃ½áÂÛ£®

½â´ð ½â£º£¨1£©¡ßÍÖÔ²µÄÀëÐÄÂÊΪ$\frac{{\sqrt{2}}}{2}$£¬e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$£¬¡­¢Ù
µãA£¨1£¬$\frac{{\sqrt{2}}}{2}$£©ÊÇÍÖÔ²C£º$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1£¨a£¾b£¾0£©ÉϵÄÒ»µã£¬$\frac{1}{{a}^{2}}+\frac{1}{2{b}^{2}}=1$£¬¡­¢Ú£¬
a²=b²+c²¡­¢Û£¬½â¢Ù¢Ú¢Û£¬
¡àa=$\sqrt{2}$£¬b=1£¬c=1£¬
¡àÍÖÔ²·½³ÌΪ$\frac{{x}^{2}}{2}$+y²=1£®¡­£¨5·Ö£©
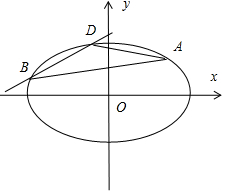
£¨2£©ÉèÖ±ÏßBDµÄ·½³ÌΪy=$\frac{\sqrt{2}}{2}$x+m£¬
ÓÉ$\left\{\begin{array}{l}{y=\frac{\sqrt{2}}{2}x+m}\\{{x}^{2}+2{y}^{2}=2}\end{array}\right.$£¬ÏûÈ¥y¿ÉµÃ£º2x²+2$\sqrt{2}$mx+2m²-2=0£¬
¡àx₁+x₂=-$\sqrt{2}$m£¬x₁x₂=m²-1£¬
ÓÉ¡÷=8m²-16£¨m²-1£©=-8m²+16£¾0£¬¿ÉµÃ-$\sqrt{2}$£¼m£¼$\sqrt{2}$£¬
¡à|BD|=$\sqrt{1+£¨\frac{\sqrt{2}}{2}£©^{2}}$|x₁-x₂|=$\frac{\sqrt{6}}{2}$$\sqrt{2{m}^{2}-4{m}^{2}+4}$=$\sqrt{3}$•$\sqrt{2-{m}^{2}}$£¬
ÉèdΪµãA£¨1£¬$\frac{{\sqrt{2}}}{2}$£©µ½Ö±ÏßBD£ºy=$\frac{\sqrt{2}}{2}$x+mµÄ¾àÀ룬¡àd=$\frac{|m|}{\sqrt{1+\frac{1}{2}}}$=$\frac{\sqrt{6}}{3}|m|$£¬
¡àS¡÷ABD=$\frac{1}{2}$|BD|d=$\frac{1}{2}¡Á\sqrt{3}\sqrt{2-{m}^{2}}¡Á\frac{\sqrt{6}}{3}|m|$=$\frac{\sqrt{2}}{2}$$\sqrt{2{m}^{2}-{m}^{4}}$£¬
µ±ÇÒ½öµ±m=¡À1¡Ê£¨-$\sqrt{2}$£¬$\sqrt{2}$£©Ê±£¬¡÷ABDµÄÃæ»ý×î´ó£¬×î´óֵΪ$\frac{\sqrt{2}}{2}$£®¡­£¨12·Ö£©

µãÆÀ ±¾ÌâÖ÷Òª¿¼²éÍÖÔ²µÄ·½³ÌµÄÇ󷨣¬¿¼²éÏÒ³¤¹«Ê½µÄÓ¦ÓúͶþ´Îº¯ÊýÇó×îÖµµÄ·½·¨£¬¿¼²é˼άÄÜÁ¦¡¢ÔËËãÄÜÁ¦ºÍ×ۺϽâÌâµÄÄÜÁ¦£®