Question

12．在平行四边形ABCD中，若$\overrightarrow{AC}$=$\overrightarrow{a}$，$\overrightarrow{BD}$=$\overrightarrow{b}$，则$\overrightarrow{AB}$=（　　）

• A． $\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$）
• B． $\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$）
• C． $\frac{1}{2}$（$\overrightarrow{b}$-$\overrightarrow{a}$）
• D． $\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$

Answer 1

分析 根据题意，设AC与BD相交与点O，分析可得$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AC}$，$\overrightarrow{BO}$=$\frac{1}{2}$$\overrightarrow{BD}$，由向量的三角形法则可得$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=$\overrightarrow{AO}$-$\overrightarrow{BO}$，代入即可得答案．

解答 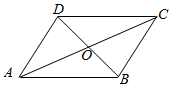解：根据题意，设AC与BD相交于点O，
则$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{AC}$，$\overrightarrow{BO}$=$\frac{1}{2}$$\overrightarrow{BD}$，
则$\overrightarrow{AB}$=$\overrightarrow{AO}$+$\overrightarrow{OB}$=$\overrightarrow{AO}$-$\overrightarrow{BO}$=$\frac{1}{2}$（$\overrightarrow{AC}$-$\overrightarrow{BD}$）=$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{b}$）；
故选：B．

点评 本题考查向量加法的几何意义，注意作出平行四边形，利用向量的加减运算的几何意义进行分析．