
分析 (1)设出直线的倾斜角,求出直线的参数方程即可;
(2)根据x=ρcosθ,y=ρsinθ求出圆的普通方程,代入直线的参数方程求出$\frac{1}{|PM|}$+$\frac{1}{|PN|}$的值即可.
解答 解:(1)设直线l的倾斜角是α,
∵直线l的方向向量为(1,$\sqrt{3}$),故tanα=$\sqrt{3}$,
∵α∈[0,π),故直线l的倾斜角是$\frac{π}{3}$,
故直线l的参数方程是$\left\{\begin{array}{l}{x=-1+tcos\frac{π}{3}}\\{y=-2+tsin\frac{π}{3}}\end{array}\right.$(t为参数),
即$\left\{\begin{array}{l}{x=-1+\frac{1}{2}t}\\{y=-2+\frac{\sqrt{3}}{2}t}\end{array}\right.$;
(2)∵ρ=2cos(θ-$\frac{π}{3}$)=cosθ+$\sqrt{3}$sinθ,
故ρ2=ρcosθ+$\sqrt{3}$ρsinθ,
故圆的普通方程是x2+y2-x-$\sqrt{3}$y=0,
将直线l的参数方程代入,整理得t2-(3+2$\sqrt{3}$)t+6+2$\sqrt{3}$=0,
设方程的两根为t1,t2,则t1+t2=3+2$\sqrt{3}$,t1t2=6+2$\sqrt{3}$,可见t1,t2均为正数,
∴$\frac{1}{|PM|}$+$\frac{1}{|PN|}$=$\frac{|PM|+|PN|}{|PM|•|PN|}$=$\frac{{t}_{1}{+t}_{2}}{{t}_{1}{•t}_{2}}$=$\frac{3+2\sqrt{3}}{6+2\sqrt{3}}$=$\frac{1+\sqrt{3}}{4}$.
点评 本题考查了参数方程以及普通方程和极坐标方程的转化,考查参数方程的应用,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | [$\frac{π}{3}$,$\frac{2π}{3}$] | B. | (0,$\frac{π}{3}$] | C. | [$\frac{2π}{3}$,π) | D. | (0,$\frac{π}{3}$]∪[$\frac{2π}{3}$,π) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$
在四棱锥P-ABCD中,底面ABCD为矩形,AB⊥PC,其中BP=BC=3,PC=$\sqrt{6}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
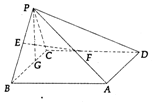
 如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥底面ABCD,E,F 分别是 AB,PC 的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,PD⊥底面ABCD,E,F 分别是 AB,PC 的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-11)∪(4,+∞) | B. | (-11,4) | C. | (-4,-3) | D. | (-∞,-4]∪[-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com