
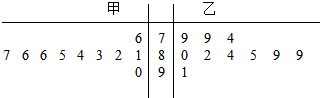
 甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示,现从这20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)=( )
甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示,现从这20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)=( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
分析 由茎叶图,确定P(A)=$\frac{1}{2}$,P(B)=$\frac{9}{20}$,P(AB)=$\frac{1}{4}$,再利用条件概率公式,即可求得结论.
解答 解:从这20名学生中随机抽取一人,基本事件总数为20个.
∵将“抽出的学生为甲小组学生”记为事件A,
∴事件A包含的基本事件有10个,故P(A)=$\frac{1}{2}$;
∵“抽出学生的英语口语测试成绩不低于85分”记为事件B,
∴事件B包含的基本事件有9个,P(B)=$\frac{9}{20}$,
又事件AB包含的基本事件有5个,故P(AB)=$\frac{1}{4}$,
故P(A|B)=$\frac{P(AB)}{P(B)}$=$\frac{5}{9}$,
故选:D.
点评 本题考查读茎叶图,考查条件概率的计算,属于中档题.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | zmin=2,zmax=3 | B. | zmin=2,无最大值 | ||
| C. | zmax=3,无最小值 | D. | 既无最大值,也无最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com