
分析 (1)可得出向量$\overrightarrow{b}$的坐标,根据$\overrightarrow{a}∥\overrightarrow{b}$及平行向量的坐标关系即可得出cosx=3sinx,从而便可得出$\frac{3sinx-cosx}{sinx+cosx}$的值;
(2)可先求出$\overrightarrow{a}+\overrightarrow{b}$的坐标,然后进行向量坐标的数量积运算,并由二倍角的正余弦公式及两角和的正弦公式即可得到$f(x)=2sin(2x+\frac{π}{6})-2m$,从而得出$m=sin(2x+\frac{π}{6})$,而可以求出sin(2x+$\frac{π}{6}$)在$[0,\frac{π}{2}]$的范围,从而可得出m的取值范围.
解答 解:(1)$m=\sqrt{3}$时,$\overrightarrow{b}=(cosx,\sqrt{3})$;
又$\overrightarrow{a}∥\overrightarrow{b}$;
∴3sinx+cosx=0;
∴cosx=-3sinx;
∴$\frac{3sinx-cosx}{sinx+cosx}=\frac{6sinx}{-2sinx}=-3$
(2)$f(x)=2(\sqrt{3}sinx+cosx,m-1)•(cosx,m)$-2m2-1
=$\sqrt{3}sin2x+cos2x+1+2{m}^{2}-2m-$2m2-1
=$2sin(2x+\frac{π}{6})-2m$
根据题意,方程$2sin(2x+\frac{π}{6})-2m=0$有解;
即m=$sin(2x+\frac{π}{6})$有解;
∵$x∈[0,\frac{π}{2}]$;
∴$2x+\frac{π}{6}∈[\frac{π}{6},\frac{7π}{6}]$
∴$sin(2x+\frac{π}{6})∈[-\frac{1}{2},1]$;
∴m的取值范围为$[-\frac{1}{2},1]$.
点评 考查向量坐标的加法和数量积的运算,向量平行时坐标的关系,以及二倍角的正余弦公式,两角和的正弦公式,以及不等式的性质,函数零点的定义,正弦函数的图象.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,6) | B. | (0,4) | C. | (0,6) | D. | (0,12) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从高一年级1500名学生中的某次数学考试成绩(单位:分)中抽取部分学生的成绩,得到频率分布直方图如图:
从高一年级1500名学生中的某次数学考试成绩(单位:分)中抽取部分学生的成绩,得到频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
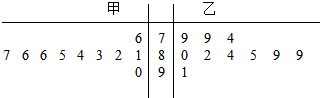 甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示,现从这20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)=( )
甲、乙两个小组各10名学生的英语口语测试成绩的茎叶图如图所示,现从这20名学生中随机抽取一人,将“抽出的学生为甲小组学生”记为事件A;“抽出的学生英语口语测试成绩不低于85分”记为事件B.则P(A|B)=( )| A. | $\frac{5}{6}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 男生 | 女生 | 总计 | |
| 收看 | 40 | ||
| 不收看 | 30 | ||
| 总计 | 60 | 110 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com