练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数.

    (1)当时，求证： ；

    (2)设函数 ，且有两个不同的零点 ，

    ①求实数的取值范围； ②求证： .

    【答案】（1）；（2）①； ②证明见解析

    【解析】试题分析：（1）构造函数，利用函数增减性求证；（2）①只需函数的极小值小于0即可；②由①知，记，分析函数的增减性，可知单调递减，所以，转化为即可求证.

    试题解析：

    （1）记，则，在上，

    即在上递减，所以，即恒成立

    记，则，在上，

    即在上递增，所以，即恒成立

    ①，定义域： ，则

    易知在递增，而，所以在上，

    在递减，在递增， ,

    要使函数有两个零点，则

    故实数的取值范围是

    ②由①知，记

    当时，由①知： ，则

    再由得，

    ，

    故恒成立， 单调递减

    ，即，而，

    ，所以，由题知， ， 在递增，所以，即

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列不等式中，解集为R的是（ ）
    A.x2+4x+4＞0
    B.|x|＞0
    C.x2＞﹣x
    D.x2﹣x+ ≥0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知如下等式： ， ， ，…当n∈N*时，试猜想12+22+32+…+n2的值，并用数学归纳法给予证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】当x∈[﹣2，1]时，不等式ax3﹣x2+4x+3≥0恒成立，则实数a的取值范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】f（x）=（ax2+x﹣1）ex
    （1）当a＜0时，求f（x）的单调区间；
    （2）若a=﹣1，f（x）的图象与g（x）= x3+ x2+m的图象有3个不同的交点，求实数m的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知A，B，C为△ABC的三个内角，且其对边分别为a，b，c，若c2+b2+cb=a2
    （1）求A；
    （2）若a=2 ，b+c=4，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC点，F棱AC上，且AF=3FC．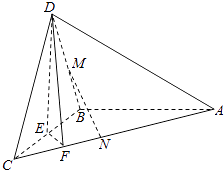

    （1）求三棱锥D﹣ABC的体积；
    （2）求证：AC⊥平面DEF；
    （3）若M为DB中点，N在棱AC上，且CN= CA，求证：MN∥平面DEF．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ，（ ）.

    （1）讨论函数在上零点的个数；

    （2）若有两个不同的零点， ，求证： .

    （参考数据： 取， 取， 取）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知a＞0，a≠1，设p：函数y=loga（x+1）在（0，+∞）上单调递减；q：曲线y=x2+（2a﹣3）x+1与x轴交于不同的两点．如果p且q为假命题，p或q为真命题，求a的取值范围．

    查看答案和解析>>

    同步练习册答案