
分析 (Ⅰ) 利用数学归纳法证明左边不等式,利用作差法证明右边不等式,即可证明:$\frac{2}{3}$<an+1<an;
(Ⅱ) 问题等价于证明Sn-$\frac{2n}{3}$<$\frac{4}{3}$,即$\sum_{i=1}^{n}$(${a}_{i}-\frac{2}{3}$)<$\frac{4}{3}$,利用放缩法、等比数列的求和公式,即可证明.
解答 证明:(Ⅰ) 先证明an+1>$\frac{2}{3}$,
n=1时,2a2=$\frac{1}{2}$+$\frac{2}{\sqrt{3}}$,∴a2=$\frac{1}{4}$+$\frac{\sqrt{3}}{3}$>$\frac{2}{3}$,结论成立,
假设n=k时,结论成立,即ak+1>$\frac{2}{3}$,
则n=k+1时,2ak+2=$\frac{1}{2}$ak+1+$\sqrt{\frac{1}{3}+{a}_{k+1}}$>$\frac{1}{3}$+1=$\frac{4}{3}$,∴ak+2>$\frac{2}{3}$,
即n=k+1时,结论成立,
∴an+1>$\frac{2}{3}$.
∴an+1-an=-$\frac{3}{4}$an+$\frac{1}{2}$$\sqrt{\frac{1}{3}+{a_n}}$<0,
∴$\frac{2}{3}$<an+1<an;
(Ⅱ) 问题等价于证明Sn-$\frac{2n}{3}$<$\frac{4}{3}$,即$\sum_{i=1}^{n}$(${a}_{i}-\frac{2}{3}$)<$\frac{4}{3}$,
设bn=an-$\frac{2}{3}$,b1=$\frac{1}{3}$,则2an+1=$\frac{1}{2}$an+$\sqrt{\frac{1}{3}+{a_n}}$可化为2bn+1=$\frac{1}{2}$bn+$\sqrt{1+{b}_{n}}$-1,
∴$\frac{{b}_{n+1}}{{b}_{n}}$=$\frac{1}{4}$+$\frac{1}{2}$•$\frac{1}{\sqrt{1+{b}_{n}}+1}$<$\frac{3}{4}$,
∴bn≤$\frac{1}{3}$•($\frac{3}{4}$)n-1,
∴Sn-$\frac{2n}{3}$<$\frac{\frac{1}{3}[1-(\frac{3}{4})^{n}]}{1-\frac{3}{4}}$<$\frac{4}{3}$,
∴Sn<$\frac{2n}{3}$+$\frac{4}{3}$.
点评 本题考查数列与不等式的综合,考查不等式的证明,考查放缩法的运用,难度大.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
 如图,在xOy平面上,点A,B在单位圆上,已知A(1,0),∠AOB=θ(0<θ<π)
如图,在xOy平面上,点A,B在单位圆上,已知A(1,0),∠AOB=θ(0<θ<π)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 25 | C. | 26 | D. | 27 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,-1)或(2,1) | B. | (-6,3) | C. | (1,2) | D. | (2,-1)或(-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
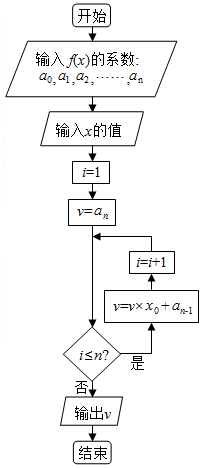
| A. | 0 | B. | 2 | C. | 3 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com