
【题目】已知项数为![]() 项的有穷数列
项的有穷数列![]() ,若同时满足以下三个条件:
,若同时满足以下三个条件:
![]() ,
,![]() 为正整数
为正整数![]() ;
;![]() 或1,其中
或1,其中![]() ,3,
,3,![]() ,
,![]() ;
;
![]() 任取数列
任取数列![]() 中的两项
中的两项![]() ,
,![]() ,剩下的
,剩下的![]() 项中一定存在两项
项中一定存在两项![]() ,
,![]() ,满足
,满足![]() ,则称数列
,则称数列![]() 为
为![]() 数列.
数列.
![]() 若数列
若数列![]() 是首项为1,公差为1,项数为6项的等差数列,判断数列
是首项为1,公差为1,项数为6项的等差数列,判断数列![]() 是否是
是否是![]() 数列,并说明理由.
数列,并说明理由.
![]() 当
当![]() 时,设
时,设![]() 数列
数列![]() 中1出现
中1出现![]() 次,2出现
次,2出现![]() 次,3出现
次,3出现![]() 次,其中
次,其中![]() ,
,![]() ,
,![]() .
.
求证:![]() ,
,![]() ,
,![]() ;
;
![]() 当
当![]() 时,求
时,求![]() 数列
数列![]() 中项数
中项数![]() 的最小值.
的最小值.
【答案】(1)数列![]() 不是
不是![]() 数列; (2)见解析; (3)2027.
数列; (2)见解析; (3)2027.
【解析】
![]() 根据
根据![]() 数列的定义判断即可;
数列的定义判断即可;
![]() 根据
根据![]() 数列的定义证明即可;
数列的定义证明即可;
![]() 先证明项数
先证明项数![]() 的最小值是2027:再证明上述数列是
的最小值是2027:再证明上述数列是![]() 数列,从而判断即可.
数列,从而判断即可.
![]() 若数列
若数列![]() :1,2,3,4,5,6是
:1,2,3,4,5,6是![]() 数列,
数列,
取数列![]() 中的两项1和2,
中的两项1和2,
则剩下的4项中不存在两项![]() ,
,![]() ,
,
使得![]() ,故数列
,故数列![]() 不是
不是![]() 数列;
数列;
![]() 若
若![]() ,对于
,对于![]() ,
,![]() ,若存在
,若存在![]() ,满足
,满足![]() ,
,
![]() ,于是
,于是![]() ,
,![]() ,
,
故![]() ,
,![]() ,从而
,从而![]() ,矛盾,
,矛盾,
故![]() ,同理
,同理![]() ,
,
下面证明![]() :
:
若![]() ,即2出现了1次,不妨设
,即2出现了1次,不妨设![]() ,
,![]() ,
,
等式左边是3,等式右边有几种可能,分别是![]() 或
或![]() 或
或![]() ,
,
等式两边不相等,矛盾,于是![]() ;
;
![]() 设出现
设出现![]() 次,2出现
次,2出现![]() 次
次![]() ,
,
2019出现![]() 次,其中
次,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由![]() 可知,
可知,![]() ,
,![]() ,且
,且![]() ,同理
,同理![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,
故项数![]() ,
,
下面证明项数![]() 的最小值是2027:
的最小值是2027:
取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可以得到数列![]() :1,1,1,1,2,2,3,
:1,1,1,1,2,2,3,![]() ,2016,2017,2018,2019,2019,2019,2019,
,2016,2017,2018,2019,2019,2019,2019,
接下来证明上述数列是![]() 数列:
数列:
若任取的两项分别是1,1,则其余的项中还存在2个1,满足![]() ,
,
同理,若任取的两项分别是2019,2019也满足要求,
若任取的两项分别是1,2,则其余的项中还存在3个1,1个2,满足要求,
同理,若任取的两项分别是2018,2019也满足要求,
若任取![]() ,
,![]() ,则在其中的项中取
,则在其中的项中取![]() ,
,![]() ,满足要求,
,满足要求,
同理,若![]() ,
,![]() 也满足要求,
也满足要求,
若任取的两项![]() ,
,![]() 满足
满足![]() ,
,
则在其余的项中选取![]() ,
,![]() ,
,
每个数最多被选取了1次,于是也满足要求,
从而,项数![]() 的最小值是2027.
的最小值是2027.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
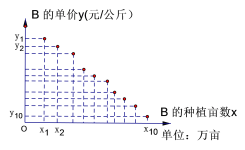
【题目】某地种植常规稻A和杂交稻B,常规稻A的亩产稳定为500公斤,统计近年来数据得到每年常规稻A的单价比当年杂交稻B的单价高50%.统计杂交稻B的亩产数据,得到亩产的频率分布直方图如下;统计近10年来杂交稻B的单价(单位:元/公斤)与种植亩数(单位:万亩)的关系,得到的10组数据记为![]() ,并得到散点图如下,参考数据见下.
,并得到散点图如下,参考数据见下.
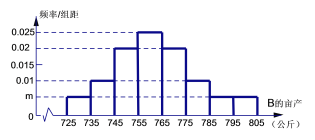
(1)求出频率分布直方图中m的值,若各组的取值按中间值来计算,求杂交稻B的亩产平均值;
(2)判断杂交稻B的单价y(单位:元/公斤)与种植亩数x(单位:万亩)是否线性相关,若相关,试根据以下统计的参考数据求出y关于x的线性回归方程;
(3)调查得到明年此地杂交稻B的种植亩数预计为2万亩,估计明年常规稻A的单价,若在常规稻A和杂交稻B中选择,明年种植哪种水稻收入更高?
统计参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
附:线性回归方程![]() ,
,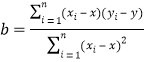 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
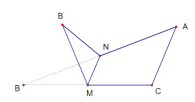
【题目】如图,∠C=![]() ,
,![]() ,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为
,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为
的长轴长为![]() ,右顶点到左焦点的距离为
,右顶点到左焦点的距离为![]() ,直线l:
,直线l:![]() 与椭圆
与椭圆![]() 交于A,B两点.
交于A,B两点.

![]() 求椭圆
求椭圆![]() 的方程;
的方程;
![]() 若A为椭圆的上项点,M为AB中点,O为坐标原点,连接OM并延长交椭圆
若A为椭圆的上项点,M为AB中点,O为坐标原点,连接OM并延长交椭圆![]() 于N,
于N,![]() ,求k的值.
,求k的值.
![]() 若原点O到直线l的距离为1,
若原点O到直线l的距离为1,![]() ,当
,当![]() 时,求
时,求![]() 的面积S的范围.
的面积S的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②函数![]() ,的最小值是3
,的最小值是3
③用长为![]() 的铁丝围成--个平行四边形,则该平行四边形能够被直径为
的铁丝围成--个平行四边形,则该平行四边形能够被直径为![]() 的圆形纸片完全覆盖
的圆形纸片完全覆盖
④已知正实数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,点
,点![]() ,
,![]() .
.
(1)若线段![]() 的中垂线与圆
的中垂线与圆![]() 相切,求实数
相切,求实数![]() 的值;
的值;
(2)过直线![]() 上的点
上的点![]() 引圆
引圆![]() 的两条切线,切点为
的两条切线,切点为![]() ,若
,若![]() ,则称点
,则称点![]() 为“好点”. 若直线
为“好点”. 若直线![]() 上有且只有两个“好点”,求实数
上有且只有两个“好点”,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com