
���� ��1������������������������������ʽ��ͬ�����Ǻ����Ļ�����ϵ���tanx��ֵ���ɵ�x��ֵ��
��2������������������������ʽ�����Ǻ�ȱ任������f��x��=$\overrightarrow{a}•\overrightarrow{b}$�Ľ���ʽ�����������Һ����ĵ�������ú���g��x���ĵ������ԣ�
��� �⣺��1����������$\overrightarrow{a}$=��$\sqrt{3}$sinx��sinx����$\overrightarrow{b}$=��cosx��sinx����
�ٸ���|$\overrightarrow{a}$|=|$\overrightarrow{b}$|���ɵ�3sin2x+sin2x=cos2x+sin2x�����tanx=��$\frac{\sqrt{3}}{3}$��
�ٸ���x��[0��$\frac{��}{2}$]���ɵ�x=$\frac{��}{6}$��
��2���ߺ���f��x��=$\overrightarrow{a}$$•\overrightarrow{b}$=$\sqrt{3}$sinxcosx+sin2x=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1-cos2x}{2}$=sin��2x-$\frac{��}{6}$��+$\frac{1}{2}$��
��x��[0��$\frac{��}{2}$]����2x-$\frac{��}{6}$��[-$\frac{��}{6}$��$\frac{5��}{6}$]����sin��2x-$\frac{��}{6}$����[-$\frac{1}{2}$��1]��f��x����[0��$\frac{3}{2}$]��
f��x����ͼ������ƽ��$\frac{��}{6}$����λ��õ�g��x��=sin[2��x+$\frac{��}{6}$��-$\frac{��}{6}$]+$\frac{1}{2}$=sin��2x+$\frac{��}{6}$��+$\frac{1}{2}$��
��2k��+$\frac{��}{2}$��2x+$\frac{��}{6}$��2k��+$\frac{3��}{2}$��k��z����� k��+$\frac{��}{6}$��x��k��+$\frac{2��}{3}$���ʺ���g��x���ļ�����Ϊ[k��+$\frac{��}{6}$��k��+$\frac{2��}{3}$]��k��z��
�ٽ��x��[0��$\frac{��}{2}$]���ɵú���g��x���ļ�����Ϊ[$\frac{��}{6}$��$\frac{��}{2}$]��
ͬ����ú���g��x����������Ϊ[0��$\frac{��}{6}$]��
���� ������Ҫ�������������������������㣬ͬ�����Ǻ����Ļ�����ϵ�����Ǻ�ȱ任�����Һ����ĵ������䣬�����е��⣮


 һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д� Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��1�� | B�� | ��0��1] | C�� | ��-�ޣ�0���ȣ�1��+�ޣ� | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=cos��x-$\frac{3��}{2}$�� | B�� | y=sin2x-cos2x | C�� | y=cos2$\frac{x}{2}$ | D�� | y=tan2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
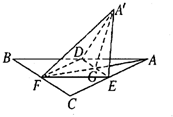 ��ͼ���ȱ�������ABC������AF����λ��DE�ཻ��G����֪��A��ED�ǡ�ADE��DE��ת�����е�һ��ͼ�Σ����������У�������ǣ�������
��ͼ���ȱ�������ABC������AF����λ��DE�ཻ��G����֪��A��ED�ǡ�ADE��DE��ת�����е�һ��ͼ�Σ����������У�������ǣ�������| A�� | ����ֱ��A��E��BD�����ܴ�ֱ | |
| B�� | ����ƽ��A��GF��ƽ��BCDE | |
| C�� | ����A��-EFD����������ֵ | |
| D�� | ����A����ƽ��ABC�ϵ���Ӱ���߶�AF�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -11 | B�� | -8 | C�� | 5 | D�� | 11 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com